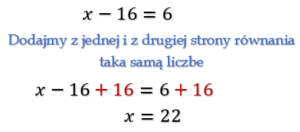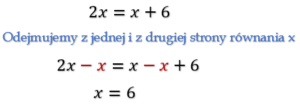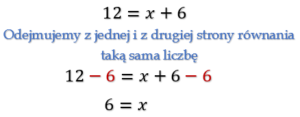Wyrażenia algebraiczne. Równania

Wyrażenia algebraiczne

Witamy w algebrze!!!

Od tego momentu będzie to nieodzowna część matematyki, w której dużo „pracujemy” na literkach. Niejednokrotnie, w dotychczasowej nauce matematyki, korzystaliście z wyrażeń algebraicznych. Były one dostępne m.in. na geometrii, w postaci wzorów do obliczania pola czy obwodu.

Najprostszymi wyrażeniami algebraicznymi są:

litery ( $x, \, y,\, z$ ),
liczby ( $0,125,\,\, \frac{3}{7},\,5$ ) oraz
połączone działaniami litery z liczbami ( $a+6,\, \frac{x}{7}, \, m^{2}$ ).

Jak stworzyć wyrażenie algebraiczne?

Spróbujmy zapisać sumę dwóch liczb $a$ i $b$ , mianowicie $a+b$ . I w taki oto sposób, udało nam się zapisać pierwsze wyrażenie algebraiczne. Spróbujmy zapisać wzór na pole prostokąta o bokach długości $a$ i $b$ , mianowicie $a\cdot b$ . W ten oto sposób otrzymamy kolejne wyrażenie algebraiczne.

Przy zapisie wyrażenia algebraicznego w postaci iloczynu nieraz możemy pominąć znak mnożenia. Zamiast $1\cdot x\cdot y$ zapiszemy $xy$ pomijając znaki mnożenia oraz jedynkę lub $\frac{3\cdot a}{5}=\frac{3a}{5}$ . Jednak musimy pamiętać, że chociaż znaku mnożenia nie widać, to jest to iloczyn!

Wyrażenie algebraiczne jest uporządkowane kiedy w iloczynie występuje najpierw liczba, a później litery, w kolejności alfabetycznej:

$9xz^{3},\: 0,25xz^{3},\: \frac{1}{7}xz^{3}$

Jeżeli, litery występujące w wyrażeniu zastąpimy liczbami, to po wykonaniu odpowiednich obliczeń otrzymamy wartość wyrażenia algebraicznego.

Obliczmy wartość wyrażenia algebraicznego $a+3b$ dla $a=1,\: b=\left ( -1 \right )$

$1+3\cdot \left ( -1 \right )=1+\left ( -3 \right )=1-3=-2$

Wyrażenia algebraiczne nazywamy wyrazami podobnymi, gdy w iloczynach występują litery, w tych samych potęgach, różniące się jedynie liczbami np:

$5a^{2}bc,\: \frac{3}{4}a^{2}bc,\: 0,33a^{2}bc$

$9xz^{3},\: 0,25xz^{3},\: \frac{1}{7}xz^{3}$

Jeśli już pogrupujemy wyrazy podobne to możemy wykonywać działania, na kilku wyrażeniach algebraicznych. Pamiętajcie o wykonywaniu działań zgodnie z kolejnością. W taki sposób, otrzymamy wyrażenie algebraiczne, zapisane w prostszej postaci.

$a+b+c+4a-3b+2c=(1+4)a+(1-3)b+(1+2)c=$

$=5a+(-2)b+3c=5a-2b+3c$

Równania

Równanie to nic innego jak przyrównane jednego wyrażenie algebraicznego do innego wyrażenia algebraicznego.

Aby rozwiązać dane równanie musimy znaleźć liczbę, która je spełnia.

Znajdź liczby spełniające przykładowe równania:

$a+6=10$

Aby znaleźć właściwe rozwiązanie musimy odpowiedzieć na pytanie: Jaką liczbę należy dodać do 6, aby otrzymać 10?

Odpowiedź nasuwa się automatycznie: musi to być liczba $4$ .

$b-5=2$

Patrząc na przykład powyżej odpowiedzmy na pytanie: Od jakiej liczby musimy odjąć 5, żeby otrzymać 2?

Oczywiście od 7.

$10-c=2$

Analogicznie jak powyżej jaką liczbę należy odjąć od 10, żeby otrzymać 2?

Tak dokładnie, chodzi o 8.

$5\cdot d=30$

Jaka liczbę należy pomnożyć przez 5, aby otrzymać 30?

Oczywiście, jest tylko jedna możliwość, mianowicie 6.

$e:10=4$

Jaką liczbę należy podzielić przez 10, aby otrzymać wynik 4?

Oczywiście, szukana liczba to 40.

$100:f=4$

Przez jaka liczbę należy podzielić 100, aby otrzymać 4?

Odpowiedź jest prosta. Szukana liczba to 25.

Prawda, że proste jest rozwiązywanie nieskomplikowanych równań. W wielu przypadkach można od razu podać wynik. Niestety, nie zawsze jest tak łatwo.

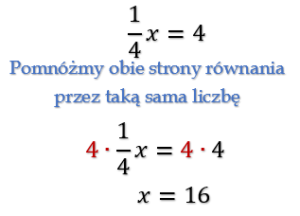
Pamiętajmy, że równanie nie zmieni swojego rozwiązania jeśli dodamy, odejmiemy, pomnożymy lub podzielimy obie jego strony przez tę samą liczbę. Poniżej przedstawiam kilka sposobów dzięki, którym nawet skomplikowane równanie stanie się łatwe do rozwiązania.

Strony równania możemy zamieniać $x=6$ to jest to samo co $6=x$ .

Jest jeszcze jedna rzecz, która jest często pomijana przez uczniów i jest to błąd. Mianowicie, jeśli już znaleźliśmy rozwiązanie równania, to należy sprawdzić czy jest to rozwiązanie prawidłowe. Aby to zrobić, wstawiamy nasz wynik do jednej strony równania początkowego i sprawdzamy czy wynik pokrywa się z drugą stroną tego równania.

Znajdźmy x:

$\frac{3}{4}x=12$ (mnożymy obie strony równania przez $\frac{4}{3}$ , bądź dzielimy przez $\frac{3}{4}$ to już jak komuś wygodnie)