Czym się różni prosta od odcinka?
Prosta nie ma początku, ani końca. Odcinek ma początek i koniec. Jest jeszcze półprosta, która ma początek i nie ma końca lub ma koniec, ale nie ma początku.
Co to są proste prostopadłe i jak je narysować szybko i sprawnie?
Proste i
są prostopadłe, jeśli przecinają się pod kątem prostym.
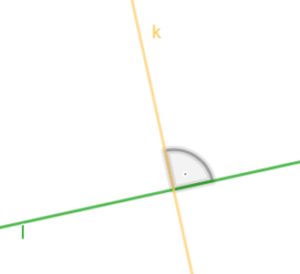
oznaczamy .
Dwa odcinki są prostopadłe, gdy leżą na prostych prostopadłych.
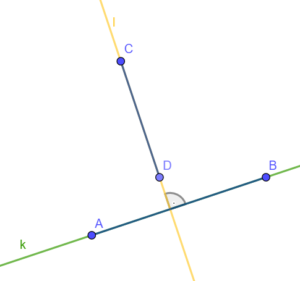
oznaczamy .
Aby narysować proste prostopadłe potrzebujemy ekierki. Rysujemy dowolna prostą. Potem dokładamy ekierkę kątem prostym do prostej . Następnie rysujemy odcinek wzdłuż boku ekierki, który nie leży na narysowanej prostej.
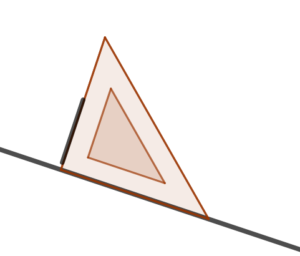
Na koniec przesuwamy ekierkę i przedłużamy odcinek tak, aby powstała prosta przecinająca początkową prostą.
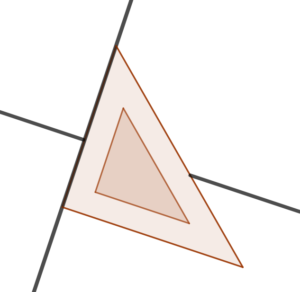
Co to są proste równoległe i jak je narysować?
Proste i
są równoległe, wtedy gdy nie mają wspólnych punktów lub gdy się pokrywają.
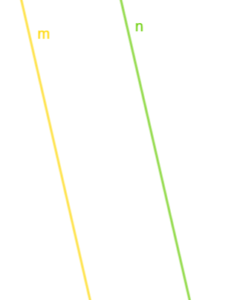
Oznaczamy je . Każda prosta jest równoległa sama do siebie.
Dwa odcinki są równoległe, gdy leżą na prostych równoległych
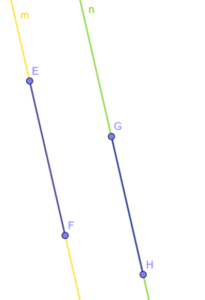
oznaczamy je .
Aby narysować dwie proste równoległe będziemy potrzebować linijki i ekierki. Zaczynamy od narysowania dowolnej prostej. Następnie dokładamy ekierkę bokiem (przy kącie prostym) do naszej narysowanej prostej. Kolejno do naszej ekierki dokładamy linijkę.
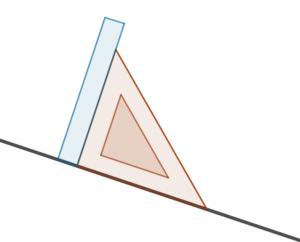
Teraz trzymamy linijkę i przesuwamy ekierkę w górę lub w dół, i zaznaczamy odcinek równoległy.
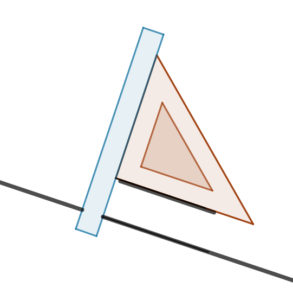
Kończąc dokładamy linijkę do odcinka i przedłużamy go rysując prostą równoległą do początkowej.
Odległość punktu od prostej
- Jest to długość najkrótszy prostopadłego odcinek, który łączy nasz punkt z prostą.
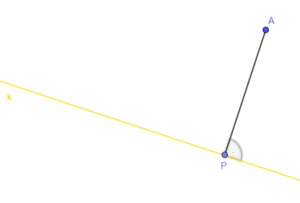
Długość odcinka to odległość między punktami i
. Oznaczamy
.
Odległość dwóch prostych równoległych, to długość najkrótszego odcinka prostopadłego do prostych.
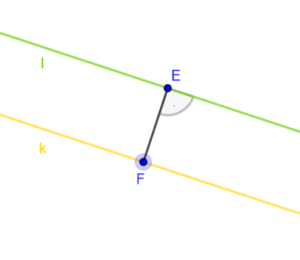
Długość odcinka, to odległość między punktami i
. Oznaczamy
.
Kąty
Kąt to każda część płaszczyzny, którą wyznaczają dwie półproste (ramiona kąta) o wspólnym początku (wierzchołek kąta).
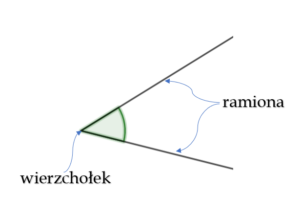
UWAGA: dwie półproste o wspólnym początku tworzą tak naprawdę dwa kąty.
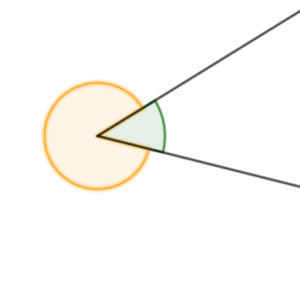
Rodzaje kątów:
- zerowy– ma miarę równą
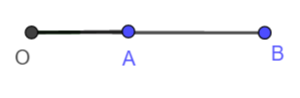
- ostry – ma miarę mniejszą niż
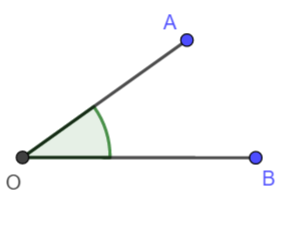
- prosty – ma miarę równą
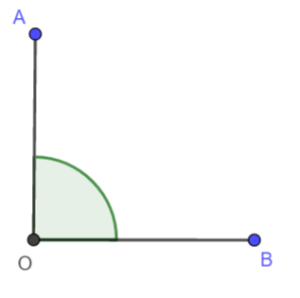
- rozwarty – ma miarę większą niż
i mniejszą niż
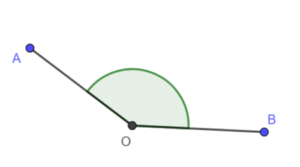
- półpełny – ma miarę równą
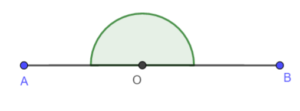
- wklęsły – ma miarę większą niż
i mniejszą niż
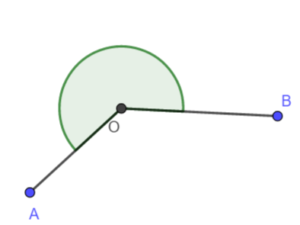
- pełny – ma miarę równą
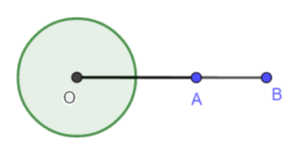
- wypukły – każdy kąt, który nie jest wklęsły jest wypukły.
Kąty przyległe – kąty, które razem tworzą kąt i maja jedno wspólne ramię
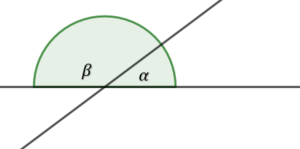
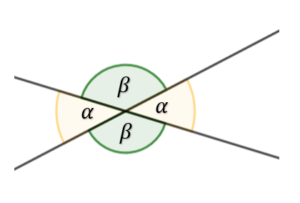
Kąty wierzchołkowe – są to kąty, które leżą na przeciwko siebie, a ich ramiona są częściami przecinających się prostych
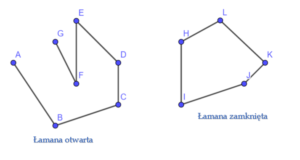
Łamana – to figura składająca się z odcinków, takich że dwa dowolne jej odcinki mają wspólny punkt i koniec jednego odcinka jest początkiem drugiego (z wyjątkiem ostatniego odcinka).
Wielokąt jest to część płaszczyzny ograniczona łamaną zamkniętą razem z tą łamaną. Czyli wszystkie punkty, które leżą w jego wnętrzu i na bokach.
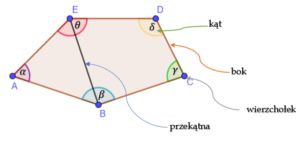
Przekątna wielokąta to odcinek łączący dwa wierzchołki wielokąta, który nie jest jego bokiem.
Obwód wielokąta to suma długości wszystkich boków.
Wielokąt, który ma wszystkie boki takiej samej długości i wszystkie kąty wewnętrzne takiej samej miary nazywamy wielokątem foremnym.
Wielokąty foremne:
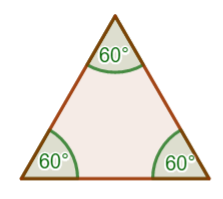
trójkąt równoboczny
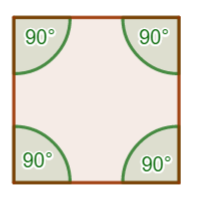
kwadrat
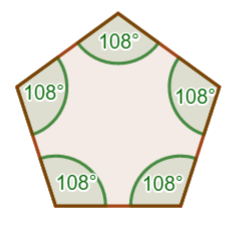
pięciokąt foremny
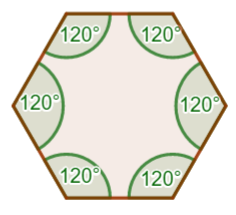
sześciokąt foremny
Was this helpful?
2 / 0