Pola wielokątów - Matma.com.pl

Przypomnijmy sobie jakie jednostki służą do określania pola powierzchni. Są to:

milimetry kwadratowe ( $mm^{2}$ ) , $1\, mm^{2}$ to pole kwadratu o boku $1\, mm$
centymetry kwadratowe ( $cm^{2}$ ), $1\, cm^{2}$ to pole kwadratu o boku $1\, cm$
decymetry kwadratowe ( $dm^{2}$ ), $1\, dm^{2}$ to pole kwadratu o boku $1\, dm$
metry kwadratowe ( $m^{2}$ ), $1\, m^{2}$ to pole kwadratu o boku $1\, m$
kilometry kwadratowe ( $km^{2}$ ), $1\, km^{2}$ to pole kwadratu o boku $1\, km$
ar oznaczamy symbolem $a$ i jest to pole powierzchni kwadratu o boku $10\, m$

$1\, a=10\, m\cdot 10\, m=100\, m^{2}$

hektar oznaczamy symbolem $ha$ i jest to pole powierzchni kwadratu o boku $100\, m$

$1\, ha=100\, m\cdot 100\cdot m=10\, 000\, m^{2}$

$1\, ha=100\, a$

Aby zamienić większą jednostkę pola na mniejszą i się przy tym nie pomylić nie trzeba się uczyć na pamięć. Wystarczy stosować zależności jakie występują między jednostkami. Poniżej kilka przykładowych zamian:

$1\, m^{2=}(100\, cm)^{2}=10\, 000cm^{2}$

$5\, dm^{2}=5\cdot 1\, dm^{2}=5\cdot (10\,cm )^{2}=5\cdot 100\, cm^{2}=500\, cm^{2}$

$8\, cm^{2}=8\cdot 1\, cm^{2}=8\cdot (10\, mm^{2})=8\cdot 100\, mm^{2}=800\, mm^{2}$

Pamiętajmy, że istota matematyki polega na zrozumieniu istniejących faktów, a nie na uczeniu się na pamięć!

Pole prostokąta

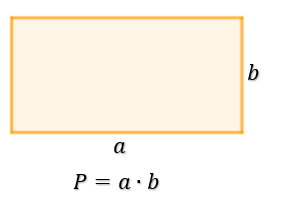
Pole kwadratu

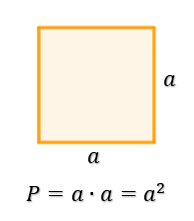
Pole równoległoboku

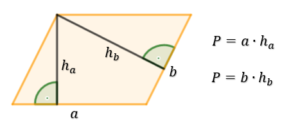
Skąd taki wzór?

Weźmy dowolny równoległobok i przetnijmy go wzdłuż jednej wysokości

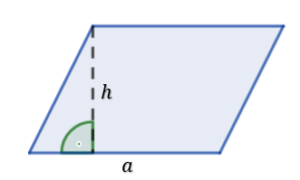
Następnie złóżmy nasze dwie części w prostokąt.

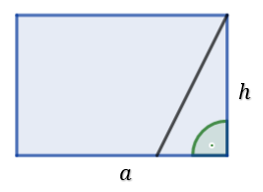
Teraz widzimy skąd mamy wzór na pole równoległoboku.

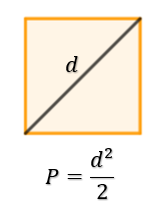
Pole rombu

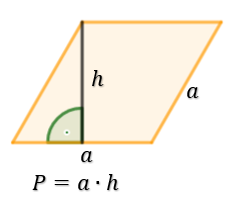
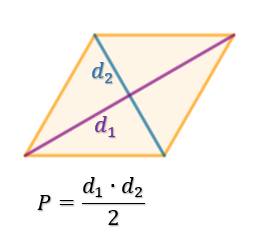
Skąd takie wzory?

Pierwszy wzór, można wyprowadzić analogicznie, jak wzór na pole równoległoboku. Zajmijmy się drugim wzorem z przekątnymi rombu.

Weźmy dwa jednakowe romby i jeden z nich przetnijmy wzdłuż przekątnych

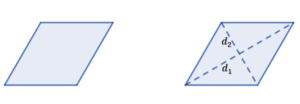
Następnie złóżmy prostokąt z otrzymanych elementów

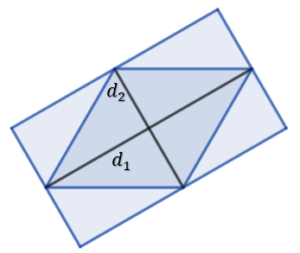
pole naszego prostokąta to $P=d_{1}\cdot d_{2}$

Jednak, ze względu na to, że mieliśmy dwa romby otrzymane pole dzielimy na dwa. Czyli otrzymujemy $P=\frac{d_{1}\cdot d_{2}}{2}$

Pole trójkąta

Jeśli weźmiemy dwa jednakowe trójkąty to możemy je złożyć w równoległobok.

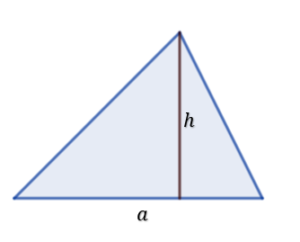
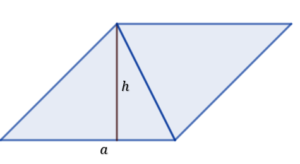
Widzimy, że powstał nam równoległobok, a obliczenie jego pola już nie stanowi problemu $P=a\cdot h$

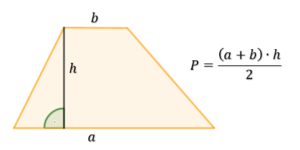
Pole trapezu

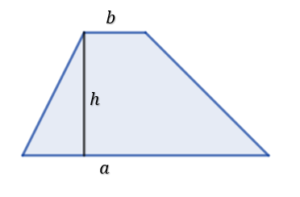
Podobnie jak z trójkątem, jeśli weźmiemy dwa jednakowe trapezy to możemy je złożyć w równoległobok.

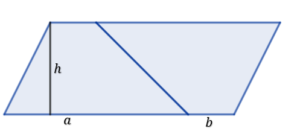
Widzimy, że powstał nam równoległobok o jednym boku długości $a+b$ . Obliczenie jego pola już nie stanowi problemu $P=\frac{\left (a+b \right )\cdot h}{2}$

Pole dowolnego wielokąta

Aby obliczyć pole dowolnego wielokąta należy podzielić go na znane przez nas wielokąty. Następnie obliczyć pola mniejszych wielokątów i zsumować otrzymane pola.

Was this helpful?

0 / 0