Przypomnijmy sobie poznane już figury przestrzenne i ich własności. Jeśli ktoś przysypiał w klasie piątej teraz ma okazje nadrobić zaległości.
Graniastosłup prosty ma dwie takie same podstawy, które są równoległe. W jego podstawie może być dowolny wielokąt. Ściany boczne graniastosłupa prostego są prostokątami i są one prostopadłe do podstaw.
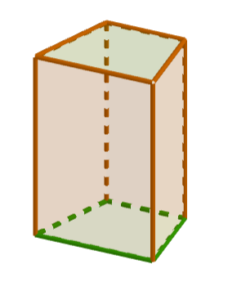
Jeśli w podstawie graniastosłupa prostego będzie prostokąt, to taki graniastosłup nazywamy prostopadłościanem. W bryłach tych każdą ścianę można uznać za podstawę.
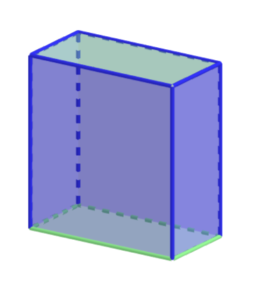
Jeśli wszystkie ściany prostopadłościanu będą kwadratami to taki graniastosłup nazywamy sześcianem.
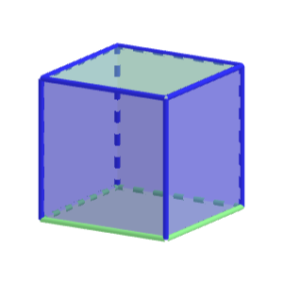
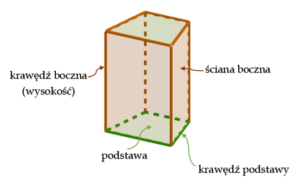
W każdym graniastosłupie prostym mamy:
- dwie postawy będące wielokątami;
- ściany boczne prostopadłe do podstaw;
- odcinek, który łączy podstawy i jest do nich prostopadły nazywany wysokością graniastosłupa.
Graniastosłup trójkątny
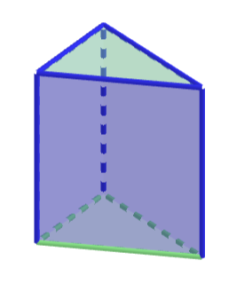
ściany: 5
krawędzie: 9
wierzchołki: 6
Graniastosłup czworokątny
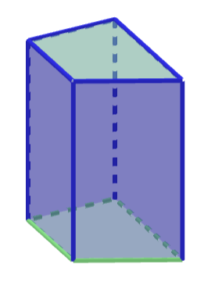
ściany: 6
krawędzie: 12
wierzchołki: 8
Graniastosłup pięciokątny
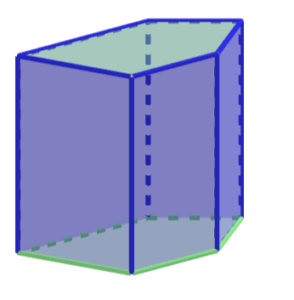
ściany: 7
krawędzie: 15
wierzchołki: 10
Graniastosłup sześciokątny
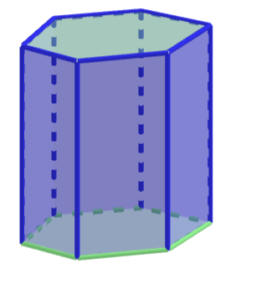
ściany: 8
krawędzie: 18
wierzchołki: 12
Aby obliczyć pole powierzchni całkowitej graniastosłupa musimy dodać do siebie pola wszystkich ścian graniastosłupa. Tak więc, jest to suma pól dwóch podstaw oraz wszystkich ścian bocznych.
to pole powierzchni podstawy
to pole powierzchni bocznej, czyli suma pól wszystkich ścian bocznych
Pole powierzchni całkowitej sześcianu
to pole powierzchni dowolnej ściany sześcianu
Objętość graniastosłupa to iloczyn jego pola podstawy i długości wysokości graniastosłupa
to pole powierzchni podstawy
to wysokość graniastosłupa
Objętość sześcianu
– długość krawędzi sześcianu
Aby obliczyć objętość posługujemy się jednostkami objętości:
– 1 milimetr sześcienny (sześcian o boku
)
– 1 centymetr sześcienny (sześcian o boku
) jest to inaczej
, czyli jeden mililitr
waży
– 1 decymetr sześcienny (sześcian o boku
) jest to inaczej
, czyli jeden litr
waży
Jeden hektolitr to jednostka sto razy większa od litra zapisujemy
– 1 metr sześcienny (sześcian o boku
)
– 1 kilometr sześcienny (sześcian o boku
)
Was this helpful?
0 / 0