Liczby wymierne - wprowadzenie

Dotychczas poznaliśmy różne liczby, mianowicie:

liczby naturalne $\mathbb{N}=\left \{ 0,1,2,3,... \right \}$
liczby całkowite $\mathbb{Z}=\left \{ ...,-2,-1,0,1,2,,,, \right \}$
ułamki zwykłe i dziesiętne

Wszystkie te liczby tworzą razem zbiór liczby wymiernych. Czyli zbiór liczb, które można przedstawić w postaci ilorazu liczb całkowitych.

W zbiorze liczb wymiernych możemy dodawać, odejmować, mnożyć i dzielić jednocześnie pamiętając o kolejności wykonywania działań.

Przypomnijmy sobie kilka istotnych informacji, z poprzednich lat, odnośnie liczb, aby obliczenia na liczbach wymiernych szły nam sprawnie.

Kolejność wykonywania działań:
- najpierw wykonujemy działania w nawiasach;
- mnożenie i dzielenie wykonujemy przed dodawaniem i odejmowaniem;
- potęgowanie wykonujemy przed mnożeniem i dzieleniem.

$\frac{1}{2}+\left ( 4^{_{2}} :2-2\right )=\frac{1}{4}+\left ( 16:2-2 \right )=\frac{1}{4}+\left ( 8-2 \right )=\frac{1}{4}+6=6\frac{1}{4}$

Opuszczanie nawiasów:
- jeśli przed nawiasem jest znak plus to wynik działania w nawiasie pozostaje taki sam;

$3+\left ( \frac{1}{4} \cdot 1,6\right )=3+\left ( \frac{1}{4} \cdot \frac{16}{10}\right )=3+\left (\frac{1}{\cancel{4}}\cdot \frac{\cancel{4}}{5} \right )=3+\frac{1}{5}=3\frac{1}{5}$

- jeśli przed nawiasem jest znak minus to znak wyniku działania w nawiasie zmieniamy na przeciwny;

$-\left ( 3-\frac{2}{3} \right )=-\left ( 2\frac{3}{3}-\frac{2}{3} \right )=-\left ( 2\frac{1}{3} \right )=-2\frac{1}{3}$

Liczby przeciwne to dwie liczby leżące na osi liczbowej w takiej samej odległości od zera. Suma liczb przeciwnych jest równa zero.

Zamiana ułamka zwykłego na dziesiętny i odwrotnie. Nie każdy ułamek zwykły można zamienić na dziesiętny, ale każdy ułamek dziesiętny można zamienić na zwykły. Jeśli, mamy wykonać działanie, w którym jest ułamek zwykły i dziesiętny to musimy oba ułamki zapisać w jednakowej postaci.

- Jeśli chcemy zamienić ułamek dziesiętny na ułamek zwykły to należy zapisać go w postaci ułamka zwykłego, tak jak się ten ułamek dziesiętny czyta. Następnie jeśli się da to skracamy ułamek.

$0,16=\frac{\cancel{16}}{\cancel{100}}=\frac{4}{25}$

- Aby zamienić ułamek zwykły na dziesiętny możemy ten ułamek rozszerzyć tak, aby w mianowniku było 10, 100 lub 1000 i tak dalej.

$\frac{2}{5}=\frac{4}{10}=0,4$

Jeśli jest to niewykonalne wówczas musimy podzielić licznik przez mianownik. Wówczas ułamki będą miały rozwinięcie dziesiętne nieskończone (dzielenie nie ma końca). Gdy w rozwinięciu nieskończonym zaobserwujemy powtarzający się ciąg cyfr (okres) to będziemy mieli rozwinięcie nieskończone okresowe ułamka. $\frac{1}{9}=0,111...=0,(1)$

Każda liczba wymierna ma rozwinięcie dziesiętne skończone lub rozwinięcie dziesiętne nieskończone okresowe.

Działania na liczbach dodatnich i ujemnych
- - dodawanie:
    - gdy do dowolnej liczby chcemy dodać liczbę dodatnią to przesuwamy się na osi liczbowej w prawo, o tyle miejsc, ile wskazuje drugi składnik;
    - gdy chcemy dodać liczbę dodatnią do ujemnej to przesuwamy się na osi od liczby dodatniej, o tyle miejsc jaką wartość ma liczb ujemna, w lewo;
  - odejmowanie liczby można zastąpić dodawaniem liczby do niej przeciwnej;
  - mnożenie (dzielenie) dwóch liczb o takich samych znakach zawsze jest dodatni;
  - mnożenie (dzielenie) dwóch liczb o przeciwnych znakach zawsze jest ujemny.

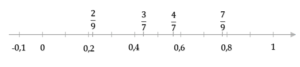
Zaznaczanie liczby wymiernej na osi liczbowej

Liczby wymierne podobnie jak liczby całkowite możemy zaznaczać na osi liczbowej. Aby dobrze to zrobić musimy wiedzieć jakie położenie będzie naszej liczby. Jeśli chodzi o liczby całkowite nie będzie to problemem. Gorzej jest w przypadku ułamków, które maja po kilka miejsc po przecinku. W takich przypadkach musimy posłużyć się przybliżeniem i zaokrąglić naszą liczbę.

Zaokrąglanie rozwinięcia dziesiętnego

Aby zaokrąglić liczbę posługujemy się symbolem” $\approx$ “, który czytamy: równy w przybliżeniu.

Najpierw musimy wybrać do, którego miejsca zaokrąglamy naszą liczbę (pozycja cyfry w liczbie).

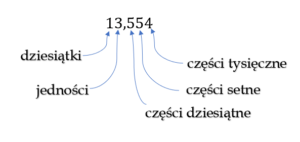
Następnie zaokrąglamy liczbę do danego miejsca, odrzucając wszystkie cyfry na prawo od naszej cyfry. W miejsca odrzuconych cyfr wstawiamy zera. Jeśli pierwsza z odrzuconych cyfr będzie równa: