Figury płaskie i ich własności.

Figura płaska najczęściej kojarzy nam się z trójkątem, czworokątem czy innym wielokątem. Nie każdy wie, że figurami płaskimi są też: punkt, prosta, półprosta, odcinek i tak dalej.

Prosta nie ma początku, ani końca.

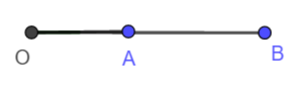
Odcinek ma początek i koniec.

Długość odcinka to odległość między punktem A, a punktem B. Oznaczamy $\left | AB \right |$ .

Jest jeszcze półprosta, która ma początek i nie ma końca lub ma koniec, ale nie ma początku.

Punkty są współliniowe, jeśli leżą na jednej prostej.

Punkty A, B, C, D są współliniowe.

Wzajemne położenie dwóch prostych:

Jeśli dwie proste się przetną, to w miejscu przecięcia powstanie ich punkt wspólny.

Proste $k$ i $l$ są prostopadłe, jeśli przecinają się pod kątem prostym.

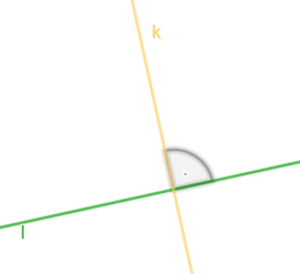
oznaczamy $k\perp l$ .

Dwa odcinki są prostopadłe, gdy leżą na prostych prostopadłych.

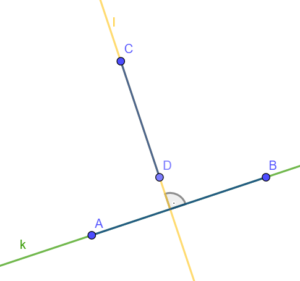
oznaczamy $AB\perp CD$ .

Proste $m$ i $n$ są równoległe, wtedy gdy nie mają wspólnych punktów lub gdy się pokrywają.

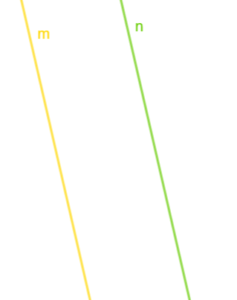
Oznaczamy je $m\parallel n$ . Każda prosta jest równoległa sama do siebie. Dwie proste równoległe nie mają punktów wspólnych.

Dwa odcinki są równoległe, gdy leżą na prostych równoległych

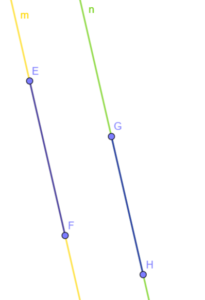
oznaczamy je $EF\parallel GH$ .

Odległość punktu od prostej

Jest to długość najkrótszy prostopadłego odcinek, który łączy nasz punkt z prostą.

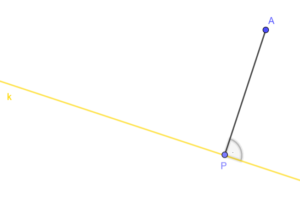
Długość tego odcinka, to odległość między punktami $A$ i $P$ . Oznaczamy $\left | AP \right |$ .

Odległość dwóch prostych równoległych, to długość najkrótszego odcinka prostopadłego do prostych.

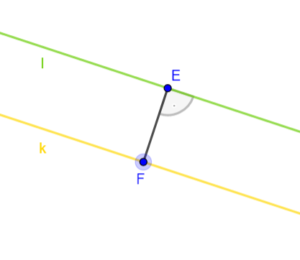
Długość tego odcinka, to odległość między punktami $E$ i $F$ . Oznaczamy $\left | EF \right |$ .

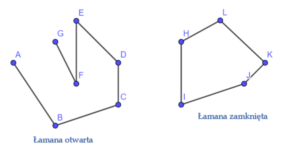
Łamana – to figura składająca się z odcinków, takich że dwa dowolne jej odcinki mają wspólny punkt i koniec jednego odcinka jest początkiem drugiego (z wyjątkiem ostatniego odcinka).

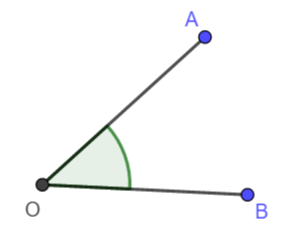
Kąt to każda część płaszczyzny, którą wyznaczają dwie półproste (ramiona kąta), o wspólnym początku (wierzchołek kąta).

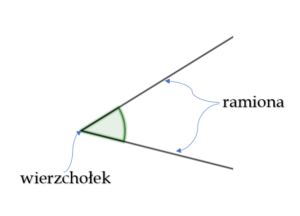
UWAGA: dwie półproste o wspólnym początku tworzą, tak naprawdę, dwa kąty.

Najczęściej, żeby oznaczyć kąty używamy liter alfabetu greckiego: $\alpha ,\, \beta, \, \gamma, \, \delta \,$ , i tak dalej

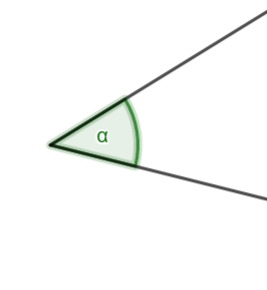
lub trzech dużych liter, na przykład: $AOB$ (gdzie $A$ i $B$ to punkty znajdujące się na ramionach kąta, a $O$ to wierzchołek kąta).

Rodzaje kątów:

kąt zerowy – kąt którego ramiona się pokrywają. Ma on miarę równą $0^{\circ }$ ;

kąt pełny – składa się z całej płaszczyzny i ramiona tego kata się pokrywają. Ma on miarę równą $360^{\circ }$ ;

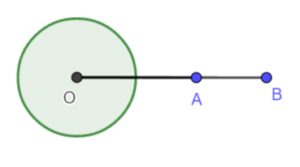
kąt półpełny – ramiona tego kąta tworzą prostą. Ma on miarę równą $180^{\circ }$ ;

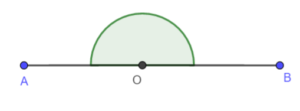
prosty – ramiona tego kąta są prostopadłe. Ma on miarę równą $90^{\circ }$ ;

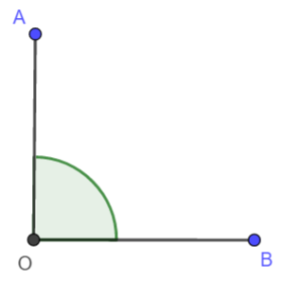
ostry – jest większy od kąta zerowego, ale mniejszy od kąta prostego. Kąt ostry ma mniej niż $90^{\circ }$ ;

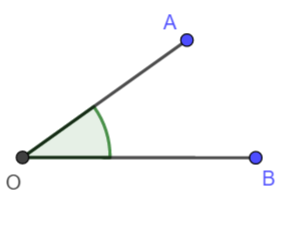
rozwarty – jest większy od kata prostego, ale mniejszy od kąta półpełnego;

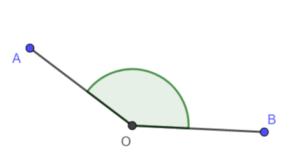
wklęsły – jest większy od kąta półpełnego, ale mniejszy od kąta pełnego;

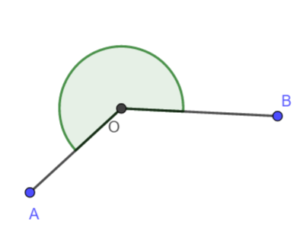
wypukły – każdy kąt, który nie jest wklęsły jest wypukły tj. kąt zerowy, pełny, półpełny, prosty, ostry i rozwarty.

Zamiast pisać kąt $\alpha$ ma miarę $60^{\circ }$ napiszemy $\alpha =60^{\circ }$ . Natomiast zamiast kąt $AOB$ ma $135^{\circ }$ zapiszemy $\sphericalangle AOB=135^{\circ}$ .

Jeśli dwa kąty maja taka samą miarę, to nazywamy je kątami przystającymi.

Kąty utworzone przez proste:

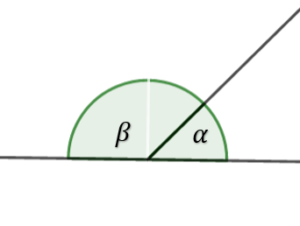
kąty przyległe – są to kąty, które tworzą razem kąt półpełny i maja jedno wspólne ramię (przylegają do siebie). Dwa kąty przyległe tworzą kąt półpełny.

$\alpha +\beta =180^{\circ }$

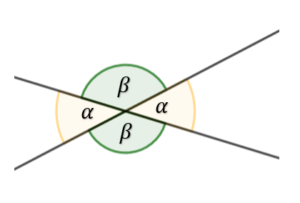
kąty wierzchołkowe – są to kąty, które leżą na przeciwko siebie, a ich ramiona są częściami przecinających się prostych. Kąty wierzchołkowe maja równe miary.

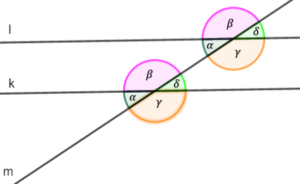
kąty naprzemianległe – kąty utworzone przez dwie proste równoległe przecięte trzecia prostą;

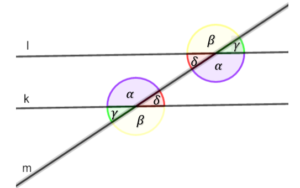
kąty odpowiadające – kąty utworzone przez dwie proste równoległe przecięte trzecia prostą.

Was this helpful?

1 / 0