System rzymski. Własności liczb naturalnych

System rzymski

Jak sama nazwa wskazuje system rzymski wprowadzili starożytni Rzymiani,e około 500 r. p.n.e.. Do zapisu liczb w systemie rzymskim używamy siedmiu znaków, mianowicie:

I	V	X	L	C	D	M
1	5	10	50	100	500	1000

Aby poprawnie posługiwać się tymi liczbami musimy stosować się do kilku zasad:

Obok siebie możemy umieścić trzy jednakowe znaki spośród: $I, X, C, M$ :
Obok siebie nie możemy umieścić dwóch takich samych znaków spośród: $V, L, D$ :
Gdy po znaku większym występuje znak mniejszy, wówczas dodajemy do siebie wartości tych znaków np. $X V = 10 + 5 = 15$
Gdy przed znakiem większym występuje znak mniejszy, wówczas od wartości większej odejmujemy mniejszą, przy czym taka kolejność może występować tylko sześć razy, mianowicie:
IV-5-1=4
IX=10-1=9
XL=50-10=40
XC=100-10=90
CD=500-100=400
CM=1000-100=900

Cyfry rzymskie zostały wyparte z codziennego życia przez cyfry arabskie, chociaż stosujemy je nadal, na przykład w zapisywaniu miesięcy zamiast czerwiec piszemy $V I$ , a zamiast grudzień $X I I$ . Warto pamiętać, że to nie Arabowie stworzyli cyfry arabskie, tylko Hindusi. Arabowie natomiast „przywieźli” je na nasz kontynent, w $X$ wieku, a konkretnie był to francuski mnich Gerbert, który później został papieżem, ale to już inny temat.Posługując się powyższymi zasadami największa liczba jaką możemy zapisać w systemie rzymskim to $M M M C M X C I X = 3999$ . Pewnie ciekawi was jak radzili sobie Rzymianie, w takiej sytuacji, gdy chcieli zapisać większa liczbę? A więc, zaczęli używać poziomej kreski, którą zapisywali nad daną liczba, a oznaczała ona, nie mniej nie więcej, tylko tyle, że liczba ta jest 1000 razy większa, np. $C = 1000 \cdot 100 = 100000$

Własności liczb naturalnych

Zbiór liczb naturalnych, to zbiór liczb zaczynających się od zera, a każda następna liczba jest o jeden większa od poprzedniej, czyli 0, 1, 2, 3, 4, … 99, 100, … Zbiór liczb naturalnych oznaczamy symbolem $\mathbb{N}$ . Najmniejszą liczbą naturalna jest $0$ , natomiast największa liczba, z tego zbioru, nie istnieje, ze względu na to, że jest ich nieskończenie wiele.

Liczbę naturalną, która dzieli bez reszty inną liczbę naturalna nazywamy jej dzielnikiem. W matematyce występują liczby doskonałe (perfect number), czyli takie liczby naturalne, które są równe sumie wszystkich swoich dzielników mniejszych od niej samej. Przykładem liczby doskonałej jest 28 (dzielniki: 1, 2, 4, 7, 14, 28). Dodając jej dzielniki, bez jej samej, otrzymujemy 1 + 2 + 4 + 7 + 14 = 28.

Największym wspólnym dzielnikiem dwóch liczb w skrócie NWD jest to największa taka sama liczba spośród dzielników dwóch liczb.

Najlepiej zobrazuje to przykład przedstawiony poniżej:

Weźmy dwie dowolne liczby 28 i 35. Pierwszym krokiem będzie wypisanie dzielników dla 28. Będą to liczby 1, 2, 4, 7, 28. Następnie wypisujemy dzielniki dla 35. Będą nimi 1, 5, 7, 35. Kolejnym krokiem jest wybranie największej wspólnej liczby dla obu cyfr. W tym wypadku będzie to 7. To właśnie 7 jest największym wspólnym dzielnikiem 28 i 35.

Możemy to zapisać symbolicznie NWD(28 , 35) = 7.

Mówiąc, o liczbach naturalnych musimy pamiętać także, co to są liczby pierwsze i liczby złożone. Liczba naturalna, która dzieli się tylko przez 1 i przez sama siebie jest liczbą pierwszą. A co kiedy liczba naturalna ma więcej, niż te dwa dzielniki? Wówczas każdą taką liczbę nazywamy liczbą złożoną. Musimy pamiętać, że ani 0, ani 1 nie są liczbami pierwszymi i nie są też liczbami złożonymi.

Rozkład liczby naturalnej na czynniki pierwsze to inaczej zapisanie tej liczby w postaci iloczynu liczb pierwszych (od najmniejszej do największej). Jak to zrobić? A więc, bierzemy dowolną liczbę naturalną, na przykład 138 i zapisujemy ją w postaci iloczynu (niekoniecznie liczb pierwszych), czyli 138 = 2· 69. Następnie, próbujemy rozłożyć liczbę złożoną z naszego iloczynu, czyli 69 na iloczyn liczb naturalnych i tak dalej, aż finalnie dojdziemy do iloczynu, który składa się z samych liczb pierwszych. W naszym przypadku 128 = 2 · 3 · 23

Jest jeszcze inna metoda znajdywania rozkładu liczby na czynniki pierwsze i z doświadczenia wiem, że uczniowie wolą z niej korzystać. Weźmy sobie liczbę 168 i rozłóżmy ją na czynniki naturalne. 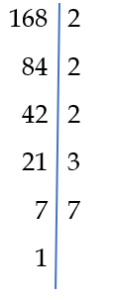Jak widać, zaczynamy od znalezienia najmniejszej liczby pierwszej, która dzieli naszą liczbę naturalną.

Wynik zapisujemy pod naszą liczbą i znowu szukamy najmniejszej naturalnej liczby dzielącej otrzymaną liczbę i tak dalej, aż dochodzimy do 1.

Spisując iloczyn liczb znajdujących się po prawej stronie kreski, otrzymujemy rozkład liczby na czynniki pierwsze. 168= 2 · 2 · 2 · 3 · 7

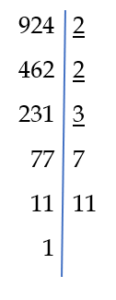
Jeszcze jedna bardzo ważna informacja. Musimy sobie uświadomić, że rozkład na czynniki naturalne jest jednoznaczny. Co to znaczy? To znaczy, że aby zapisać taki rozkład, nie można użyć innych liczb pierwszych niż te, które tworzą dany rozkład liczby na czynnik pierwsze. Oczywiście, możemy liczby pierwsze zapisać w innej kolejności, ale wiadomo, że mnożenie jest przemienne i nic to nie zmieni. Korzystając z rozkładu na czynniki pierwsze możemy szybko znaleźć największy wspólny dzielnik dwóch liczb 20 i 924:

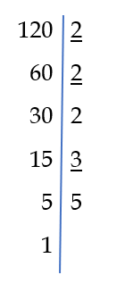Największy wspólny dzielnik, to iloczyn powtarzających się dzielników (podkreślone liczby).

NWD( 120, 924 ) = 2 · 2 · 3 = 12

Dla dociekliwych postaram się to krótko wyjaśnić, dlaczego 1 nie może być liczbą pierwszą. Podstawowe twierdzenie arytmetyki mówi o tym, że rozkład na czynniki pierwsze jest jednoznaczny. Co to tak naprawdę oznacza? A więc, weźmy, na przykład liczbę 24 i rozłóżmy ja na czynniki pierwsze, czyli $24 = 2 \cdot 2 \cdot 2 \cdot 3$ . Widzimy, że w tym rozkładzie mamy zawsze trzy dwójki i jedną trójkę, i jakbyśmy go nie zapisali, w takiej, czy innej kolejności zawsze będzie taki sam wynik. Gdyby 1 była liczba pierwszą ten sam rozkład moglibyśmy zapisać tak $24 = 1 \cdot 2 \cdot 2 \cdot 2 \cdot 3$ , ale to to samo, co $24 = 1 \cdot 1 \cdot 2 \cdot 2 \cdot 2 \cdot 3$ i $24 = 1 \cdot 1 \cdot 1 \cdot 2 \cdot 2 \cdot 2 \cdot 3$ i tak dalej. Ten przykład pokazuje dlaczego jedynka nie jest liczba pierwszą. Gdyby tak było wtedy rozkład liczby na czynniki pierwsze nie byłby jednoznaczny.

Cechy podzielności liczb naturalnych

Liczba naturalna jest podzielna przez:

2, gdy jej ostatnią cyfrą jest 2, 4, 6, 8 lub 0;

Przykładem są wszystkie liczby naturalne parzyste oprócz zera.

3, gdy suma jej cyfr jest liczba podzielna przez 3;

Weźmy dwie dowolne liczby i sprawdźmy czy są one podzielne przez 3. Na przykład: liczby 942 i 128. Zaczynamy od obliczenia sumy cyfr liczby 942, czyli 9 + 4 +2 = 15. Następnie, uzyskany przez nas wynik 15 próbujemy podzielić bez reszty przez 3 (15 : 3 = 5). Ponieważ 5 nie ma reszty, więc liczba 942 jest podzielna przez 3. Teraz spróbujmy, w podobny sposób, przeanalizować liczbę 128. Najpierw obliczmy sumę cyfr liczby 128, czyli 1 + 2 + 8 = 11. Teraz sprawdzamy, czy otrzymany przez nas wynik 11 dzieli się bez reszty przez 3. Widzimy, że 11 : 3 = 3 reszty 2, czyli liczba 128 nie jest podzielna przez 3.

4, gdy dwie ostatnie cyfry tworzą liczbę, która jest podzielna przez 4;

Sprawdzimy czy liczba 512 jest podzielna przez 4. Na początek, spójrzmy na dwie ostatnie cyfry tej liczby. Tworzą one liczbę 12, a ponieważ 12 : 4 =3 więc liczba 512 jest podzielna przez 4.

5, gdy jej ostatnią cyfrą jest 5 lub 0;

Niezmiernie łatwo jest znaleźć liczbę podzielną przez 5. Wystarczy, że spojrzymy na ostatnią cyfrę danej liczby. Jeśli będzie to 0 lub 5, wówczas taka liczba jest podzielna przez 5. Na przykład 155 lub 1200 są to liczby podzielne przez 5. Z kolei liczby 503 lub 5552 już nie są podzielne przez 5.

9, gdy suma jej cyfr jest podzielna przez 9;

Dla podzielności przez 9 postępujemy podobnie jak przy podzielności przez 3. Najpierw, liczymy sumę cyfr danej liczby i jeśli ta suma jest podzielna przez 9 to liczba jest podzielna przez 9. Weźmy dwie dowolne liczby 639 i 1281 i sprawdźmy ich sumy cyfr. Dla 639 mamy 6 + 3 + 9 = 18 i widzimy, że 18 dzieli się bez reszty przez 9, ponieważ 18 : 9 = 2 czyli liczba 639 jest podzielna przez 9. Dla 1281 mamy 1 + 2 + 8 + 1 = 12 i widzimy, że 12 nie dzieli się bez reszty przez 9 ponieważ 12 : 9 = 1 reszty 3 czyli liczba 1281 nie jest podzielna przez 9.

10, gdy jej ostatnia cyfrą jest 0;
100, gdy jej dwie ostatnie cyfry to 00;

Wielokrotność dowolnej liczby naturalnej otrzymujemy mnożąc naszą liczbę przez kolejne liczby naturalne, zaczynając od zera. Najlepiej zilustruje to przykład przedstawiający osiem kolejnych wielokrotności liczb 3 i 12

wielokrotności liczby 3 to 0, 3, 6, 9, 12, 15, 18, 21

wielokrotności liczby 12 to 0, 12, 24, 36, 48, 60, 72, 84.

A jak znaleźć czterokrotność liczby 20? Należy pomnożyć 4· 20 = 80. A więc, czterokrotność 20 to 80.

Analogicznie pięciokrotność liczby 17 to 5· 17 = 85.

Skoro już wiemy, co to jest wielokrotność liczby naturalnej znalezienie najmniejszej wspólnej wielokrotności dwóch liczb nie powinno nam sprawić problemu. Chodzi o to, aby wypisać wielokrotności danych liczb i znaleźć tę najmniejszą, która występuje w wielokrotnościach jednej i w wielokrotnościach drugiej liczby. To właśnie będzie najmniejsza wspólna wielokrotność NWW, tych dwóch liczb. PAMIĘTAJCIE, że najmniejsza wspólna wielokrotność nie może być zerem, czyli pomijamy zero szukając tej wielkości, w wielokrotnościach danych liczb. Wracając do naszych liczb, z przykładu wyżej, NWW(3 ; 12) = 12.

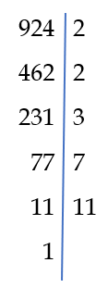
Korzystając z rozkładu na czynniki pierwsze możemy szybko znaleźć najmniejszą wspólną wielokrotność dwóch liczb

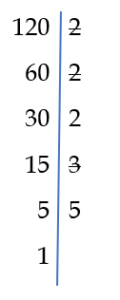Najmniejszą wspólną wielokrotność wyznaczamy wykreślając w rozkładzie mniejszej liczby te dzielniki, które występują w rozkładzie większej liczby i mnożymy większą liczbę przez te dzielniki, które nie zostały skreślone w liczbie mniejszej.

NWW(120 , 924) = 924 · 2 · 5 = 9240

Reguły kolejności wykonywania działań:

nawiasy informują nas o tym, że działania w nich wykonujemy w pierwszej kolejności;
potęgowanie i pierwiastkowanie ma pierwszeństwo przed mnożeniem, dzieleniem, dodawaniem i odejmowaniem;
mnożenie i dzielenie są to działania, które wykonujemy przed dodawaniem i odejmowaniem, ale gdy występuje mnożenie obok dzielenia wówczas wykonujemy je po kolei, tak jak występują – od lewej strony;
dodawanie i odejmowanie działania, które wykonujemy na samym końcu, natomiast gdy występują jedno obok drugiego to wykonujemy je po kolei, tak jak występują – od lewej strony.

Was this helpful?

16 / 1