Potęgi. Notacja wykładnicza

Potęga to nic innego jak wielokrotny iloczyn jednakowych czynników.

$a^{1}=a$ pierwsza potęga liczby $a$

$a^{2}=a\cdot a$ druga potęga liczby $a$

$a^{3}=a\cdot a\cdot a$ trzecia potęga liczby $a$

$\vdots$

$a^{n}=a\cdot a\cdot ...\cdot a$ n-ta potęga liczby $a$

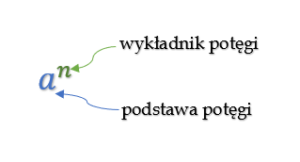
n-ta potęga liczby. a to iloczyn n czynników a.

Dowolna liczba podniesiona do potęgi zero zawsze da nam wynik 1.

$a^{0}=1$

Pamiętaj, że potęgowanie $0^{0}$ nie jest wykonalne!

Druga potęga dowolnej liczby nazywana jest kwadratem tej liczby.

$8^{2}=64$

Trzecia potęga dowolnej liczby nazywana jest sześcianem tej liczby.

$3^{3}=27$

Parzysta potęga każdej liczby jest liczbą dodatnią.

$5^{3}=5\cdot 5\cdot 5=125$

$\left ( -\frac{1}{2} \right )^{4}=\left ( -\frac{1}{2} \right )\cdot \left ( -\frac{1}{2} \right )\cdot \left ( -\frac{1}{2} \right )\cdot \left ( -\frac{1}{2} \right )=\frac{1}{16}$

Nieparzysta potęga liczby ujemnej jest liczba ujemną.

$\left (-0,1 \right )^{3}=\left (-0,1 \right )\cdot \left (-0,1 \right )\cdot \left (-0,1 \right )=-0,001$

Działania na potęgach:

$a^{m}\cdot a^{n}=a^{m+n}$

$3^{2}\cdot 3^{5}=3^{2+5}=3^{7}$

$a^{m}: a^{n}=a^{m-n}$ dla $a\neq 0$

$5^{5}:5^{2}=5^{5-2}=5^{3}$

$\left (a^{m} \right )^{n}=a^{m\cdot n}$

$\left (2^{3} \right )^{6}=2^{3\cdot 6}=2^{18}$

$\left ( a\cdot b \right )^{n}=a^{n}\cdot b^{n}$

$\left (3\cdot 10 \right )^{3}=3^{3}\cdot 10^{3}=27\cdot 1000=27000$

$\left ( a:b \right )^{n}=a^{n}:b^{n}$ dla $b\neq 0$

$\left (10:5 \right )^{3}=10^{3}:5^{3}=1000:125=8$

Oczywiście znak dzielenia możemy zastąpić kreską ułamkową.

Notacja wykładnicza

Notacja wykładnicza to notacja naukowa. Służy do zapisywania bardzo dużych lub bardzo małych wielkości. Jest to iloczyn liczby większej lub równej 1, ale mniejszej od 10 i potęgi liczby 10.

$a\cdot 10^{n}$ dla $a\geq 1\; \; i\; \; a< 10$

Spróbujmy zapisać dużą i małą liczbę w postaci notacji wykładniczej.

$3400000=3,4\cdot 10^{^{6}}$ ( przesuwamy przecinek o 6 miejsc w lewo)

$0,000053=5,3\cdot 10^{-5}$ (przesuwamy przecinek o 5 miejsc w prawo)

Was this helpful?

0 / 0

Dodaj komentarz 0