Pierwiastki - Matma.com.pl

Pierwiastki

Pierwiastkowanie to działanie odwrotne do potęgowania.

Pierwiastek kwadratowy (pierwiastek drugiego stopnia) z danej liczby nieujemnej a jest to liczba nieujemna b taka, że jej kwadrat jest równy a. Liczbę a pod pierwiastkiem nazywamy liczba podpierwiastkową.

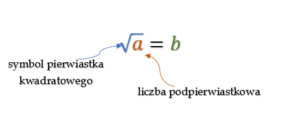
Mówiąc pierwiastek mamy na myśli pierwiastek kwadratowy. Najczęściej zapisujemy symbolem $\sqrt{ \: \: }$ . Trzeba pamiętać, że jest on jednoznaczny z zapisem $\sqrt[2]{ \: \: }$ .

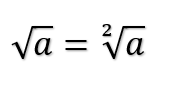
Przykłady:

$\sqrt{4}=2\; \; bo\; \; 2^{2}=4$

$\sqrt{1,69}=1,3\; \; bo\; \; \left (1,3 \right )^{2}=1,69$

$\sqrt{0}=0\; \; bo\; \; 0^{2}=0$

$\sqrt{\frac{1}{64}}=\frac{1}{8}\; \; bo\; \; \left ( \frac{1}{8} \right )^{2}=\frac{1}{64}$

Pierwiastek sześcienny (pierwiastek trzeciego stopnia) z danej liczby nieujemnej a jest to liczba nieujemna b taka, że jej sześcian (trzecia potęga) jest równy a.

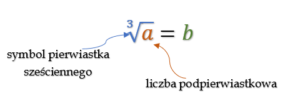
Przykłady:

$\sqrt[3]{8}=2\; \; bo\; \; 2^{3}=8$

$\sqrt[3]{-125}=-5\; \; bo\; \; \left (-5 \right )^{3}=-125$

$\sqrt[3]{0}=0\; \; bo\; \; 0^{3}=0$

$\sqrt[3]{\frac{1}{27}}=\frac{1}{3}\; \; bo\; \; \left ( \frac{1}{3} \right )^{3}=\frac{1}{27}$

Działania na pierwiastkach:

$\sqrt{a\cdot b}=\sqrt{a}\cdot \sqrt{b}$ dla $a\geq 0\; i \; b\geq 0$

$\sqrt{2500}=\sqrt{25\cdot 100}=\sqrt{25}\cdot \sqrt{100}=5\cdot 10=50$

$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$ dla $a\geq 0\; i \; b> 0$

$\sqrt{0,04}=\sqrt{\frac{4}{100}}=\frac{\sqrt{4}}{\sqrt{100}}=\frac{\cancel{2}}{\cancel{10}}=\frac{1}{5}=0,2$

$\sqrt[3]{a\cdot b}=\sqrt[3]{a}\cdot \sqrt[3]{b}$ dla dowolnych a i b

$\sqrt[3]{64000}=\sqrt[3]{64\cdot 1000}=\sqrt[3]{64}\cdot \sqrt[3]{1000}=4\cdot 10=40$

$\sqrt[3]{\frac{a}{b}}=\frac{\sqrt[3]{a}}{\sqrt[3]{b}}$ dla dowolnego a i $b\neq 0$

$\sqrt[3]{-0,125}=\sqrt[3]{-\frac{125}{1000}}=-\frac{\sqrt[3]{125}}{\sqrt[3]{1000}}=-\frac{\cancel{5}}{\cancel{10}}=-\frac{1}{2}=-0,5$

Wyłączanie czynnika przed pierwiastek

Aby wyłączyć czynnik przed pierwiastek musimy liczbę podpierwiastkową zapisać w postaci iloczynu dwóch liczb. Następnie z jednego z czynników iloczynu wyciągamy pierwiastek.

$\sqrt{40}=\sqrt{4\cdot 10}=\sqrt{4}\cdot \sqrt{10}=2\sqrt{10}$

Możemy również wykonać odwrotne działanie to znaczy wciągnąć czynnik pod pierwiastek

$2\sqrt{10}=\sqrt{4}\cdot \sqrt{10}=\sqrt{4\cdot 10}=\sqrt{40}$

Usuwanie niewymierności z mianownika

Jeśli w mianowniku ułamka mamy pierwiastek, którego nie umiemy zapisać w postaci liczby wymiernej, wówczas musimy „pozbyć się” takiego mianownika. Aby to zrobić pomnożymy licznik i mianownik przez taką samą liczbę różna od zera.

$\frac{3}{\sqrt{5}}=\frac{3}{\sqrt{5}}\cdot \frac{\sqrt{5}}{\sqrt{5}}=\frac{3\sqrt{5}}{5}$

$\frac{2}{\sqrt[3]{3}}=\frac{2}{\sqrt[3]{3}}\cdot \frac{\sqrt[3]{9}}{\sqrt[3]{9}}=\frac{2\sqrt[3]{9}}{\sqrt[3]{27}}=\frac{2\sqrt[3]{9}}{3}$

Was this helpful?

0 / 0