Proporcje - Matma.com.pl

Jeśli przyrównamy do siebie dwa ilorazy, których wynik jest taki sam

$\frac{12}{4}=3=\frac{27}{9}$

to otrzymamy proporcję.

Jeśli ilorazy $\frac{a}{b}$ i $\frac{c}{d}$ dla $b\neq 0,\; d\neq 0$ są sobie równe, to $\frac{a}{b}=\frac{c}{d}$ nazywamy proporcją.

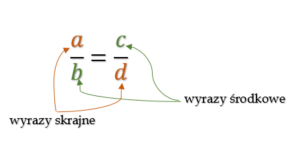
Iloczyn wyrazów skrajnych jest równy iloczynowi wyrazów środkowych.

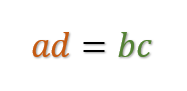
Jeśli jeden odcinek $\left | AB \right |$ mieści się kilka razy w drugim odcinku $\left | CD \right |$ to ich iloraz $\frac{\left | AB \right |}{\left | CD \right |}$ jest stosunkiem długości odcinków $\left | AB \right |$ i $\left | CD \right |$ .

Najlepiej zobrazuje to przykład.

Dana jest rurka długości 100 cm chcemy ją rozciąć na dwie części w stosunku 1:4. Jak to zrobić? Po ile centymetrów będą miały obie części naszej rurki?

Załóżmy, że $1x$ to będzie pierwsza część naszej rurki, a $4x$ to druga część. Następnie dodajmy nasze dwie części do siebie i przyrównajmy do długości rurki.