Twierdzenie Pitagorasa jest także bardzo pomocne jeśli jesteśmy w stanie wyodrębnić w jakiejś figurze płaskiej trójkąt prostokątny.
Kwadrat i twierdzenie Pitagorasa
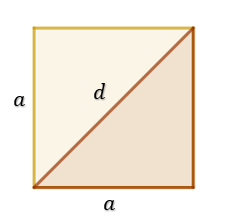
to długość przekątnej.
Widzimy, że jeśli podzielimy kwadrat na pół to otrzymamy dwa trójkąty prostokątne.
Stosując twierdzenie Pitagorasa możemy teraz bez problemu obliczyć przekątną:
Kąty w kwadracie
Jeśli poprowadzimy przekątną w kwadracie to otrzymamy dwa trójkąty prostokątne
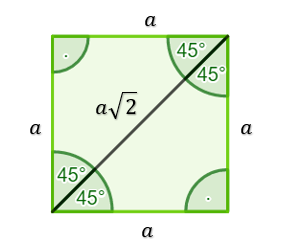
Możemy stwierdzić, że w trójkącie prostokątnym o dwóch kątach ostrych równych i przyprostokątnej równej
wszystkie boki są długości
.
Trójkąt równoboczny i twierdzenie Pitagorasa
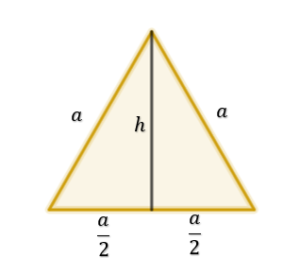
Widzimy, że jeśli zaznaczymy jedną z wysokości w trójkącie równobocznym to otrzymamy dwa trójkąty prostokątne.
Stosując twierdzenie Pitagorasa możemy teraz bez problemu obliczyć wysokość i pole.
Kąty w trójkącie równobocznym i prostokątnym
Kąty w trójkącie równobocznym są równe . Jeśli poprowadzimy wysokość to podzieli ona kąt na połowę i otrzymamy dwa trójkąty prostokątne o kątach
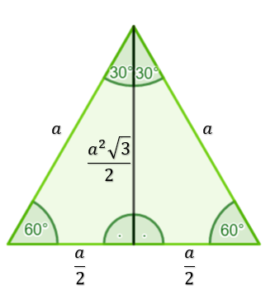
Możemy stwierdzić, że w trójkącie prostokątnym o kątach ostrych i przeciwprostokątnej długości
długości boków przyprostokątnych są równe odpowiednia: krótsza przyprostokątna
, dłuższa przyprostokątna
.
Twierdzenie Pitagorasa możemy również zastosować chcąc obliczyć długość w układzie współrzędnych.
Weźmy dowolny odcinek o początku w punkcie i końcu w punkcie
. Następnie obliczmy jego długość korzystając z twierdzenia Pitagorasa.
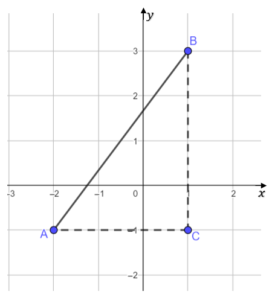
Pierwszym krokiem będzie znalezienie takiego punktu , który razem z naszymi punktami da nam trójkąt prostokątny w układzie współrzędnych.
Następnie odczytujemy długości boków i
Stosujemy twierdzenie Pitagorasa i obliczmy długość odcinka
Zatem długość odcinka wynosi 5.
Was this helpful?
0 / 1