Symetria osiowa
Jeśli jedna z figur jest odbiciem lustrzanym drugiej figury względem pewnej prostej to te figury są symetryczne względem tej prostej.
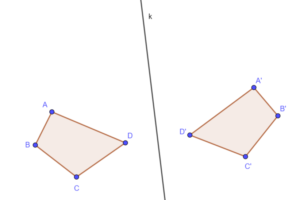
A więc każda figura symetryczna jest przystająca. ale uwaga nie odwrotnie nie każda figura przystająca jest symetryczna!
Tak samo jak z figurami jest z punktami. dwa punkty są symetryczne względem prostej jeśli
- leża na prostej prostopadłej do danej prostej
- leżą po przeciwnych stronach i w równych odległościach od danej prostej
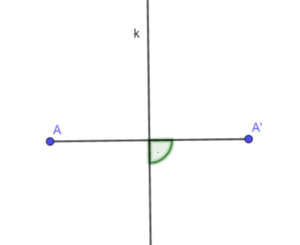
Tak samo robimy jak mamy wiele punktów.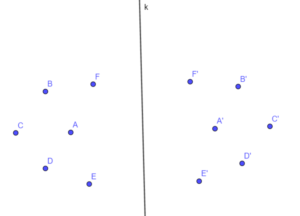
Aby dwa odcinki były symetryczne względem prostej to musimy znaleźć punkty symetryczne względem naszej prostej do końców tego odcinka i połączyć je ze sobą.
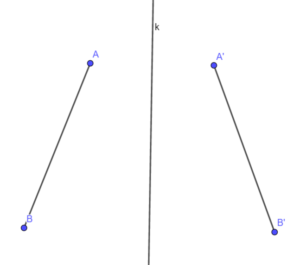
Symetralna odcinka
Symetralna odcina jest to prosta prostopadła do tego odcina i przechodząca przez jego środek.
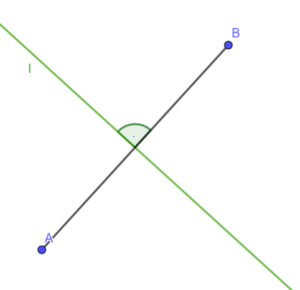
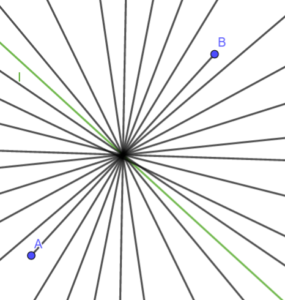
Przez środek odcinka możemy przeprowadzić nieskończenie wiele prostych ale tylko jedna z nich będzie symetralną tego odcinka.
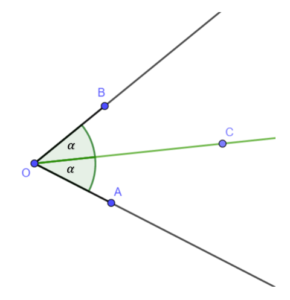
Dwusieczna kąta
Półprosta, która dzieli kąt na dwa kąty przystające nazywamy dwusieczną tego kąta.
Oś symetrii figury
Oś symetrii figury dzieli tę figurę na dwie figury przystające.
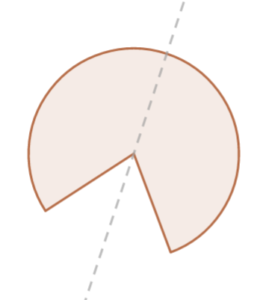
Jeśli figura ma oś symetrii to nazywamy ją osiowosymetryczną.
Nieraz figura może mieć nie jedną a kilka osi symetrii.
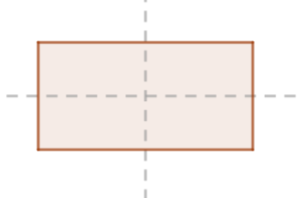
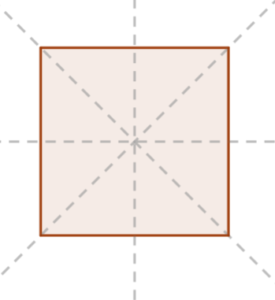
Kat ma tylko jedną oś symetrii.
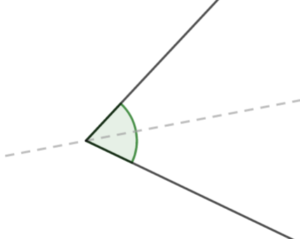
Trzeba pamiętać o różnicy między figurami dymetryczny mi względem prostej a figurą symetryczna względem prostej. Jeśli chodzi o figury symetryczne to mamy na myśli przejście jednej figury w drugą. Natomiast jeśli chodzi o jedną figurę symetryczna względem prostej to mamy na myśli odbicie lustrzane tej figury względem naszej prostek. Najważniejsze żeby nie mylić ze sobą tych dwóch pojęć.
Symetria środkowa
Symetria względem punktu to najogólniej rzecz biorąc obrót „do góry nogami”.
Dwie figury są symetryczne względem punktu gdy jedną z nich można otrzymać przez obrót drugiej o dookoła naszego punktu.

Dwa punkty A i A’ są symetryczne względem punktu S jeśli punkt S jest środkiem odcinka AA’
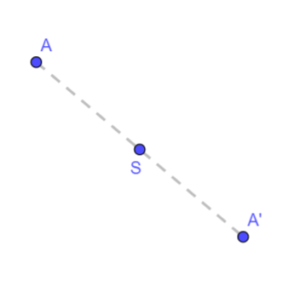
Analogiczną sytuację mamy z odcinkami symetrycznymi.
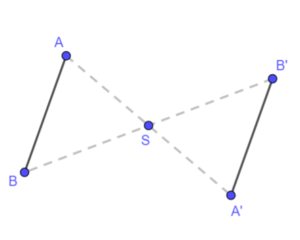
Punkt S jest środkiem symetrii figury kiedy figura i figura do niej symetryczna pokrywają się względem punktu S. Czyli jeśli obrócimy naszą figurę o to otrzymamy ta samą figurę.
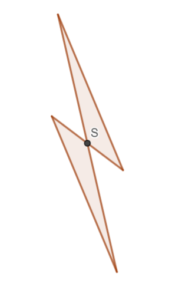
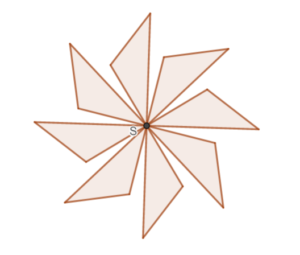
Takie figury, które mają środek symetrii nazywamy figurami środkowosymetrycznymi.
Odcinek i punkt są figurami środkowosymetrycznymi. Natomiast żaden trójką nie jest figurą środkowosymetryczną.
Was this helpful?
1 / 2