Rodzaje liczb
- liczby naturalne-są to liczby dodatnie całkowite plus zero. Zbiór liczb naturalnych możemy zapisać w postaci
- liczby całkowite- są to wszystkie liczby naturalne i ich liczby do nich przeciwne. Zbiór liczb całkowitych możemy zapisać w postaci
- liczby wymierne- są to liczby, które da się zapisać w postaci ułamka zwykłego
- liczby niewymierne- są to liczby, których nie da się zapisać w postaci ułamka zwykłego
Liczby w systemie rzymskim
| I | V | X | L | C | D | M |
| 1 | 5 | 10 | 50 | 100 | 500 | 1000 |
Aby poprawnie posługiwać się tymi liczbami musimy stosować się do kilku zasad:
- Obok siebie możemy umieścić trzy jednakowe znaki spośród: I, X, C, M
- Obok siebie nie możemy umieścić dwóch takich samych znaków spośród: V, L, D
- Gdy po znaku większym występuje znak mniejszy, wówczas dodajemy do siebie wartości tych znaków np. XV=10+5=15
- Gdy przed znakiem większym występuje znak mniejszy, wówczas od wartości większej odejmujemy mniejszą, przy czym taka kolejność może występować tylko sześć razy, mianowicie:
- IV-5-1=4
- IX=10-1=9
- XL=50-10=40
- XC=100-10=90
- CD=500-100=400
- CM=1000-100=900
System dziesiątkowy
Pamiętać należy, w którym miejscu znajduje się konkretna cyfra w danej liczbie, czyli jaką pozycje zajmuje.
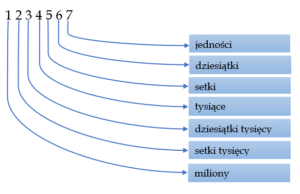
Następnie, żeby było łatwiej przeczytać dużą liczbę grupujemy ją po trzy cyfry zaczynając od końca. W naszym przypadku liczba będzie wyglądać następująco
tak zapisana cyfrę łatwo przeczytać- jeden milion dwieście trzydzieści cztery tysiące pięćset sześćdziesiąt siedem.
Zaokrąglanie liczb
Zaokrąglanie liczby jest jednym z najprostszych tematów na matematyce. Zapisując taką liczbę, zamiast znaku “=” posługujemy się symbolem” “, który czytamy: równy w przybliżeniu. Aby zaokrąglić daną liczbę, najpierw musimy wybrać do, którego miejsca zaokrąglamy naszą liczbę (pozycja cyfry w liczbie).
- Zaokrąglanie do rzędu dziesiątek – patrzymy na cyfrę jedności i jeśli, cyfra ta jest mniejsza od 5 to cyfrę dziesiątek zostawiamy bez zmian, a cyfrą jedności staje się 0 (zaokrąglamy w dół – z niedomiarem) . Jeśli, cyfra w rzędzie jedności jest większa lub równa 5 to cyfrę dziesiątek zwiększamy o jeden, a w miejscu jedności stawiamy 0 (zaokrąglenie w górę – z nadmiarem).
Analogicznie zaokrąglamy liczby do setek, tysięcy, setek tysięcy i tak dalej.
Przykład 1
Zapisz w systemie dziesiątkowym liczby
- MCDLXXIX=1000+400+50+10+10+9=1479
Zadanie 1
Zapisz w systemie dziesiątkowym liczby
-
- MCDLXX
- DCIV
- MCCXXXIV
Przykład 2
Zapisz w systemie rzymskim liczbę
- 3296=MMMCCXCVI
Zadanie 2
Zapisz w systemie rzymskim liczbę
- 1999
- 574
- największą jaką się da stosując zasady dotyczące zapisywania liczb w systemie rzymskim
Przykład 3
Ile lat minęło od roku CCLVII do roku CMXLVII
CCXLVII=247
CMXLVII=947
947-247=700
Odpowiedź: Minęło 700 lat.
Zadanie 3
- Ile lat minęło od 1 r. p. n. e. do 2 r. n.e.?
- Ile lat minęło od roku CMXLII do roku MMXIX?
Przykład 4
Zaokrąglij podaną liczbę z dokładnością do tysięcy
- 75 412≈75000
- 1 234 567≈1 235 000
Zadanie 4
Zaokrąglij liczbę 918273 z dokładnością
- do tysięcy
- do dziesiątek tysięcy
- do setek
Was this helpful?
3 / 0