III. Ułamki - Matma.com.pl

Zacznijmy od tego jak wygląda ułamek zwykły

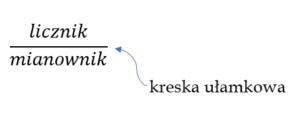
Ułamek właściwy – licznik jest mniejszy od mianownika

$\frac{2}{15}$

Ułamek niewłaściwy – licznik jest większy od mianownika

$\frac{15}{2}$

Liczba mieszana

$3\frac{1}{7}$

Porównywanie ułamków

Jeśli, ułamki mają takie same liczniki, to większy jest ten, którego mianownik jest mniejszy.

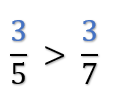
Jeśli, ułamki mają takie same mianowniki to większy jest ten, którego licznik jest większy.

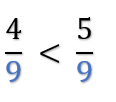
Jeśli, ułamki mają różne liczniki i mianowniki to sprowadzamy je do wspólnego licznika lub mianownika i dopiero wtedy porównujemy.

Działania na ułamkach zwykłych

Dodawanie i odejmowanie

Jeśli, ułamki właściwe mają takie same mianowniki to dodajemy lub odejmujemy liczniki, a mianownik pozostaje bez zmian.

$\frac{11}{25}+\frac{6}{25}=\frac{17}{25}$

$\frac{11}{25}-\frac{7}{25}=\frac{4}{25}$

Przed dodawaniem i odejmowaniem ułamków o różnych mianownikach sprowadzamy ułamki do wspólnego mianownika. Następnie dodajemy ułamki.

$\frac{3}{5}+\frac{2}{3}=\frac{3\cdot 3}{5\cdot 3}+\frac{2\cdot 5}{3\cdot 5}=\frac{9}{15}+\frac{10}{15}=\frac{19}{15}=1\frac{4}{15}$

$\frac{2}{3}-\frac{3}{5}=\frac{2\cdot 5}{3\cdot 5}-\frac{3\cdot 3}{5\cdot 3}=\frac{10}{15}-\frac{9}{15}=\frac{1}{15}$

Skracanie ułamków – dzielimy licznik i mianownik przez taka sama liczbę, różna od zera.

$\frac{20}{25}=\frac{4\cdot \cancel5}{5\cdot \cancel5}=\frac{4}{5}$

Rozszerzanie ułamków – mnożymy licznik i mianownik przez taka samą liczbę różną od zera.

$\frac{3}{7}=\frac{3\cdot 5}{7\cdot 5}=\frac{15}{35}$

Mnożenie

Aby pomnożyć dwa ułamki mnożymy liczniki ułamków i mianowniki ułamków. Przy mnożeniu dwóch ułamków możemy skracać licznik jednego z mianownikiem drugiego ułamka.

$\frac{3}{4}\cdot \frac{8}{9}=\frac{\cancel3}{\cancel4}\cdot \frac{2\cdot \cancel4}{\cancel3\cdot 3}=\frac{2}{3}$

Dzielenie

Aby podzielić dwa ułamki należy pierwszy ułamek pomnożyć przez odwrotność drugiego ułamka.

$\frac{6}{7}:\frac{6}{35}=\frac{\cancel6}{7}\cdot \frac{35}{\cancel6}=\frac{5\cdot \cancel7}{\cancel7}=\frac{5}{1}=5$

Jeśli, mamy wykonać mnożenie lub dzielenie liczb mieszanych musimy je najpierw zamienić na ułamki niewłaściwe.

Liczba odwrotna powstaje przez zamianę miejscami licznika z mianownikiem

Liczbą odwrotną do $\frac{3}{4}$ jest $\frac{4}{3}$

Iloczyn liczb odwrotnych jest równy 1

Ułamki dziesiętne, to liczby naturalne zapisane z użyciem przecinka. Część po lewej stronie przecinka to część całkowita, a po prawej stronie to część ułamkowa.

Jak poprawnie przeczytać taki ułamek?

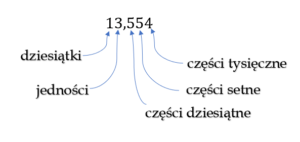
czytamy: trzynaście całych pięćset pięćdziesiąt cztery tysięczne.

Jeśli dopiszemy zero (jedno lub kilka) na końcu do naszego ułamka na przykład $13,5540$ nie zmienia to wartości tej liczby.

Porównywanie ułamków dziesiętnych

Porównujemy w pierwszej kolejności całości, jeśli są takie same, to przechodzimy kolejno do części dziesiętnych, setnych i tak dalej.

Działania na ułamkach dziesiętnych

Dodawanie i odejmowanie

Przy dodawaniu i odejmowaniu ułamków dziesiętnych dodajemy części całkowite do całkowitych, części ułamkowe do ułamkowych. Musimy pamiętać, że 10 części dziesiątych to jedna całość. Dziesięć części setnych to jedna dziesiąta. Dziesięć części tysiącznych to jedna setna i tak dalej.

Możemy też dodawać i odejmować ułamki dziesiętne pod kreskę. Należy jednak pamiętać, aby przecinek jednego ułamka była pod przecinkiem drugiego ułamka. Jeśli jeden z ułamków jest krótszy to musimy rozszerzyć taki ułamek dopisując zero na końcu.

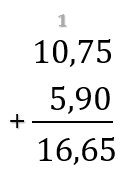
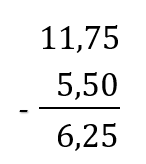
Mnożenie

Ułamki dziesiętne mnożymy tak jak liczby naturalne. Należy jednak pamiętać, aby w wyniku oddzielić przecinkiem tyle cyfr na końcu ile było łącznie w obu ułamkach.

$0,5\cdot 0,3=0,15$

Dzielenie

Najpierw rozszerzamy ułamki, tak aby dzielnik był liczbą całkowitą. Następnie wykonujemy dzielenie, tak jak dzielenie liczb naturalnych.

$0,12:0,02=12:2=6$

$0,52:0,2=5,2:2=2,6$

Jeśli, chcemy pomnożyć lub podzielić ułamek dziesiętny przez liczbę 10 należy odpowiednio przesunąć przecinek. Przy mnożeniu o jedno miejsce w prawą stronę, przy dzieleniu o jedno miejsce w lewą stronę. Przy mnożeniu przez 100 postępujemy analogicznie tylko przesuwamy przecinek o dwa miejsca. Przy mnożeniu przez 1000 o trzy miejsca. Im więcej zer, tym o więcej miejsc przesuwamy przecinek.

$1,152\cdot 10=11,52$

$1,152\cdot 100=115,2$

$1,152:10=0,1152$

$1,152:100=0,01152$

Ułamki zwykłe i dziesiętne

Jeśli, mamy wykonać działanie, w którym jest ułamek zwykły i dziesiętny to musimy oba zapisać w takiej samej postaci (zwykłej lub dziesiętnej). Każdy ułamek dziesiętny możemy zamienić na ułamek zwykły. Jednak, nie zawsze możemy zamienić ułamek zwykły na dziesiętny. Musimy pamiętać, że aby to zrobić należy ułamek rozszerzyć tak, aby w mianowniku było 10, 100 lub 1000 i tak dalej.

Rozwinięcia dziesiętne ułamków zwykłych

Aby ułamek zwykły zapisać w postaci dziesiętnej możemy podać jego rozwinięcie dziesiętne. Jak to zrobić? Wystarczy podzielić licznik przez mianownik. Jedne ułamki będą miały rozwinięcie dziesiętne skończone inne nieskończone (dzielenie nie ma końca). Zajmiemy się tymi z rozwinięciem nieskończonym. Ponieważ, te z rozwinięciem dziesiętnym skończonym można zamienić na ułamki zwykłe rozszerzając mianownik do 10, 100 lub 1000 i tak dalej.

Spróbujmy podzielić 1 przez 3:

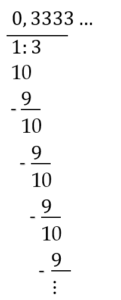
Czyli możemy zapisać:

$\frac{1}{3}=0,3333...$

W przypadku, kiedy ułamek ma rozwinięcie dziesiętne nieskończone sprawdzamy czy jakaś liczba lub kilka liczb się nie powtarza w nieskończoność. Jeśli tak będzie, to ułamek będzie miał rozwinięcie dziesiętne nieskończone okresowe.

$\frac{1}{3}=0,3333...=0,\left ( 3 \right )$

Zaokrąglanie rozwinięcia dziesiętnego

Aby zaokrąglić liczbę posługujemy się symbolem” $\approx$ “, który czytamy: równy w przybliżeniu.

Najpierw musimy wybrać do, którego miejsca zaokrąglamy naszą liczbę (pozycja cyfry w liczbie).

Następnie zaokrąglamy liczbę do danego miejsca, odrzucając wszystkie cyfry na prawo od naszej cyfry. W miejsca odrzuconych cyfr wstawiamy zera. Jeśli pierwsza z odrzuconych cyfr będzie równa: