2022 grudzień podstawa

zadanie 1. (0-1)

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Liczba $(5\cdot 5^{\frac{1}{2}})^{\frac{1}{3}}$ jest równa

A. $\sqrt[6]{5}$

B. $\sqrt[3]{25}$

C. $\sqrt{5}$

D. $\sqrt[3]{5}$

zadanie 2. (0-1)

Pan Nowak kupił obligację Skarbu Państwa za 40 000 zł oprocentowane 7% w skali roku. Odsetki są naliczane i kapitalizowane co rok.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Wartość obligacji kupionych przez pana Nowaka będzie po dwóch latach równa

A.	$40000\cdot\left ( 1,07 \right )^{2}$ zł

B.	$40000\cdot\left ( 1,7 \right )^{2}$ zł

C.	$40000\cdot\1,14$ zł

D.	$40000\cdot\1,49$ zł

zadanie 3 (0-1)

Właściciel sklepu kupił w hurtowni 50 par identycznych spodni po 𝑥 zł za parę i 40 identycznych marynarek po 𝑦 zł za sztukę. Za zakupy w hurtowni zapłacił 8000 zł. Po doliczeniu marży 50% na każdą parę spodni i 20% na każdą marynarkę ceny detaliczne spodni i marynarki były jednakowe.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Cenę pary spodni 𝑥 oraz cenę marynarki 𝑦, jaka jest konieczność w hurtowni, identyfikuje się z układem

A.	$\left\{\begin{matrix} x+y=80000\\ 0,5x=0,2y \end{matrix}\right.$
B.	$\left\{\begin{matrix} 50x+40y=80000\\ 0,5x=0,2y \end{matrix}\right.$
C.	$\left\{\begin{matrix} 50x+40y=80000\\ 1,5x=1,2y \end{matrix}\right.$
D.	$\left\{\begin{matrix} x+y=80000\\ 1,5x=1,2y \end{matrix}\right.$

Zadanie 4 (0-1)

Liczby 𝑥 i 𝑦 są pozytywne oraz 𝑥 ≠ 𝑦.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Wyrażenie $\frac{1}{x-y}+\frac{1}{x+y}$ można przekształcić do postaci

A. $\frac{2}{x-y}$

B. $\frac{2}{x^{2}-y^{2}}$

C. $\frac{2x}{x^{2}-y^{2}}$

D. $\frac{-2xy}{x+y}$

Zadanie 5 (0-1)

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Wszystkich różnych liczb czterocyfrowych, w których zapisie dziesiętnym wszystkie cyfry są różne, jest

A. $9\cdot 8\cdot 7\cdot 6$

B. $9\cdot 9\cdot 8\cdot 7$

C. $10\cdot 9\cdot 8\cdot 7$

D. $9\cdot 10\cdot 10\cdot 10$

Zadanie 6 (0-1)

Funkcja 𝑓 jest określona wzorem $f\left ( x \right )=-logx$ dla wszystkich liczb rzeczywistych
dodatnich

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Wartość funkcji 𝑓 dla argumentu $x=\sqrt{10}$ jest równa

A. $2$

B. $\left (-\frac{1}{2} \right )$

C. $\frac{1}{2}$

D. $\left ( -2 \right )$

zadanie 7

W kartezjańskim układzie współrzędnych $\left ( x,y \right )$ przedstawiono fragment wykresu funkcji kwadratowej $f\left ( x \right )=ax^{2}+bx+c$ . Wierzchołek paraboli, która jest wykresem funkcji $f$ , ma współrzędne $\left ( 5,-3 \right )$ . Jeden z punktów przecięcia paraboli z osią $Ox$ układu
współrzędnych ma współrzędne $\left ( 4,0 \right )$ .

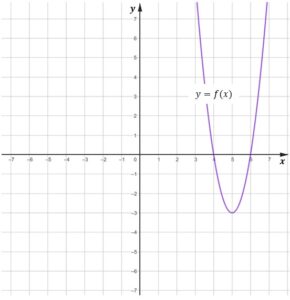zadanie 7.1 (0-1)

Zapisz poniżej zbiór wszystkich wartości funkcji $f$ .

zadanie 7.2 (0-2)

Wyznacz wzór funkcji kwadratowej $f$ w postaci kanonicznej.

Zapisz obliczenia.

zadanie 8(0-1)

Dana jest nierówność kwadratowa

$\left ( 3x-9 \right )\left ( x+k \right )< 0$

z niewiadomą $x$ i parametrem $k\in \mathbb{R}$ . Rozwiązaniem tej nierówności jest przedział $\left ( -2,3 \right )$ .

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Liczba $k$ jest równa

A. $\left ( -2 \right )$

B. $2$

C. $\left ( -3 \right )$

D. $3$

zadanie 9 (0-1)

Dana jest funkcja kwadratowa $f(x)=ax^2+bx+c$ , gdzie $a,b$ i $c$ są liczbami rzeczywistymi takimi, że $a\neq 0$ oraz $c< 0$ . Funkcja $f$ nie ma miejsc zerowych.

Dokończ zdanie tak, aby było prawdziwe. Wybierz właściwą odpowiedź A albo B oraz jej uzasadnienie1., 2. albo3.

Wykres funkcji $f$ leży w całości

nad osią $Ox$ ,

pod osią $Ox$ ,

ponieważ

$a<0$ i $b^2-4ac<0$

$a> 0$ i $b^2-4ac<0$

$a<0$ i $b^2-4ac=0$

zadanie 10 (0-1)

Dany jest układ równań

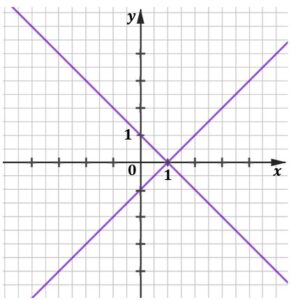
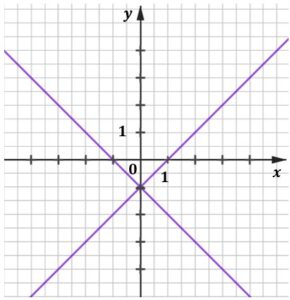
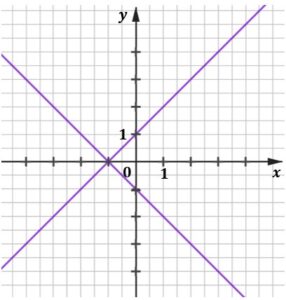
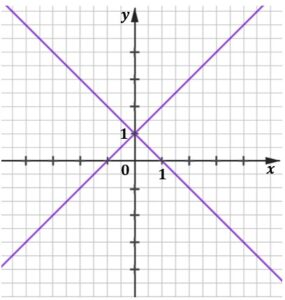
$\left\{\begin{matrix} y=x-1\\ y=-x+1 \end{matrix}\right.$

Na którym z rysunków A-D przedstawiona jest interpretacja geometryczna tego układu równań? Wybierz właściwą odpowiedź spośród podanych.

zadanie 11 (0-1)

Dany jest wielomian $W$ określony wzorem $W(x)=x^3-2x^2-3x+6$ dla każdej liczby rzeczywistej $x$ .

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Wielomian $W$ przy rozkładzie na czynniki ma postać

A. $W(x)=(x+2)(x^2-3)$

B. $W(x)=(x-2)(x^2-3)$

C. $W(x)=(x+2)(x^2+3)$

D. $W(x)=(x-2)(x^2+3)$

zadanie 12 (0-1)

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Równanie $\frac{(4-x)(2x-3)}{\left ( 3x-5 \right )(3-2x)}$ w zbiorze liczb rzeczywistych ma dokładnie

A. jedno rozwiązanie.

B. dwa rozwiązania.

C. trzy rozwiązania.

D. cztery rozwiązania.

zadanie 13 (0-1)

Dana jest nierówność

$2-\frac{x}{2}\geq \frac{x}{3}-3$

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Największą liczbą całkowitą, która spełnia tę nierówność, jest

A. $6$

B. $5$

C. $7$

D. $(-6)$

zadanie 14(0-2)

Wykaż, że dla każdej liczby naturalnej $n$ liczba $5n^2+15n$ jest podzielna przez 10.

zadanie 15 (0-1)

Dany jest ciąg $\left ( a_{n} \right )$ określony wzorem ${a_{n}}=2n^2+n$ dla każdej liczby naturalnej $n\geq 1$ .

Oceń prawdziwość podanych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe albo F- jeśli jest fałszywe.

Ciąg $\left ( a_{n} \right )$ jest malejący.

Ósmy wyraz ciągu $\left ( a_{n} \right )$ jest równy $136$ .

zadanie 16 (0-1)

Pięciowyrazowy ciąg $\left ( -3, \frac{1}{2},x,y,11\right )$ jest arytmetyczny.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Liczby $x$ oraz $y$ są równe

A. $x=4$ oraz $y=\frac{15}{2}$ .	B. $x=\frac{15}{2}$ oraz $y=4$ .
C. $x=-4$ oraz $y=\frac{15}{2}$ .	D. $x=-\frac{15}{2}$ oraz $y=4$ .

zadanie 17 (0-2)

Dany jest ciąg geometryczny $\left ( a_{n} \right )$ , określony dla każdej liczby naturalnej $n\geq 1$ . W tym ciągu $a_{1}=-5$ , $a_{2}=15$ , $a_{3}=-45$

Dokończ zdanie. Zaznacz dwie odpowiedzi tak, aby dla każdej z nich dokończenie poniższego zdania było prawdziwe.

Wzór ogólny ciągu $\left ( a_{n} \right )$ ma postać

A. $a_{n}=-5\cdot \left ( -3 \right )^{n-1}$

B. $a_{n}=-5\cdot \left ( -3 \right )^{n}$

C. $a_{n}=-5\cdot 3^{n-1}$

D. $a_{n}=-5\cdot \frac{\left ( -3 \right )^{n}}{3}$

E. $a_{n}=5\cdot \frac{\left ( -3 \right )^{n}}{3}$

F. $a_{n}=-5\cdot \left ( -3 \right )^{n}\cdot 3$

zadanie 18 (0-1)

Kąt $\alpha$ jest ostry oraz $\frac{1}{sin^{2}\alpha }+\frac{1}{cos^{2}\alpha }=\frac{16}{9}$

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Wartość wyrażenia $sin\alpha \cdot cos\alpha$ jest równa

A. $\frac{4}{3}$

B. $\frac{3}{4}$

C. $\frac{16}{9}$

D. $\frac{9}{16}$

zadanie 19 (0-1)

Punkty $A,B,C$ leżą na okręgu o środku $O$ (zobacz rysunek). Ponadto $\left | \measuredangle AOC \right |=130^{\circ }$ oraz $\left | \measuredangle BOA \right |=110^{\circ }$ .

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Miara kata wewnętrznego $BAC$ trójkąta $ABC$ jest równa

A. $60^{\circ }$

B. $55^{\circ }$

C. $50^{\circ }$

D. $65^{\circ }$

zadanie 20 (0-4)

Do wyznaczenia trzech boków pewnego kąpieliska w kształcie prostokąta należy użyć liny długości 200m. Czwarty bok tego kąpieliska będzie pokrywał się z brzegiem plaży, który w tym miejscu jest linią prostą (zobacz rysunek)

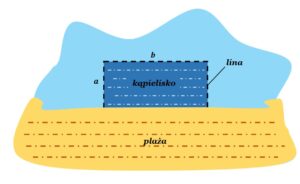Oblicz wymiary $a$ i $b$ tego kąpieliska, tak aby powierzchnia była największa

Zapisz obliczenia.

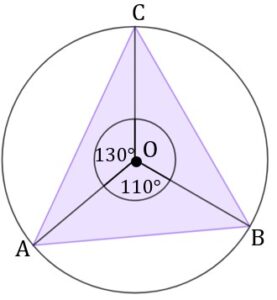
zadanie 21 (0-1)

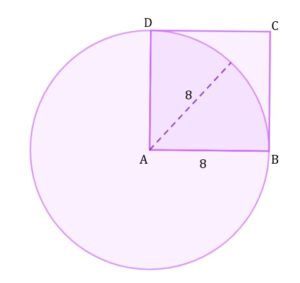
Dany jest kwadrat $ABCD$ o boku długości $8$ . Z wierzchołka $A$ zakreślono koło o promieniu równym długości boku kwadratu (zobacz rysunek)

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Pole powierzchni części wspólnej koła i kwadratu jest równe

A. $16 \pi$

B. $8\pi$

C. $4\sqrt{2}\pi$

D. $16\sqrt{2}\pi$

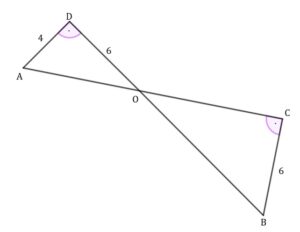
zadanie 22 (0-1)

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Długość odcinka $OD$ jest równa.

A. $9$

B. $8$

C. $2\sqrt{13}$

D. $3\sqrt{13}$

zadanie 23 (0-2)

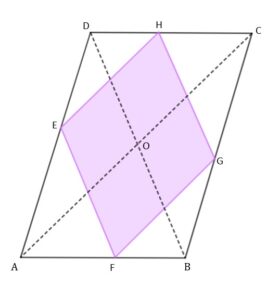
Przekątne równoległoboku $ABCD$ mają długości: $\left | AC \right |=16$ oraz $\left | BD \right |=12$ . Wierzchołki $E,F,G$ oraz $H$ rombu $EFGH$ leżą na bokach równoległoboku $ABCD$ (zobacz rysunek)

Boki rombu są równoległe do przekątnych równoległoboku.

Oblicz długość Boku rombu $EFGH$ .

Zapisz obliczenia.

zadanie 24 (0-2)

Dany jest trójkąt $ABC$ , w którym $\left | AC \right |=4$ , $\left | AB \right |=3$ , $\cos\measuredangle BAC=\frac{4}{5}$ .

Oblicz pole trójkąta $ABC$ .

Zapisz obliczenia.

zadanie 25

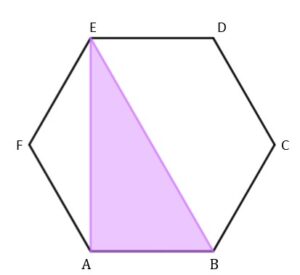Dany jest sześciokąt foremny $ABCDEF$ o polu równym $6\sqrt{3}$ (zobacz rysunek)

zadanie 25.1 (0-1)

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Pole trójkąta $ABE$ jest równe

A. $6$

B. $4\sqrt{3}$

C. $2\sqrt{3}$

D. $4$

zadanie 25.2 (0-1)

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Długość odcinka $AE$ jest równa

A. $2$

B. $2\sqrt{3}$

C. $4\sqrt{3}$

D. $4$

zadanie 26 (0-1)

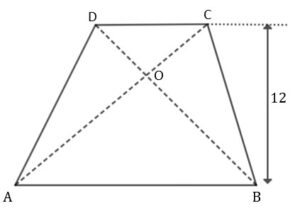
Dany jest trapez $ABCD$ , w którym $AB\parallel CD$ oraz przekątne $AC$ i $BD$ przecinają się w punkcie $O$ (zobacz rysunek). wysokość tego trapezu jest równa $12$ . Obwód trójkąta $ABO$ jest równy $39$ , a obwód trójkąta $CDO$ jest równy $13$ .

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Wysokość trójkąta $ABO$ poprowadzona z punktu $O$ jest równa

A. $3$

B. $4$

C. $9$

D. $6$

zadanie 27 (0-1)

Na płaszczyźnie w kartezjańskim układzie współrzędnych $\left ( x,y \right )$ , dany jest okrąg $O$ o równaniu

$\left ( x-3\right )^{2}+\left ( y-3 \right )^{2}=13$

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Okrąg $O$ przecina oś $Oy$ w punktach o współrzędnych

A. $\left ( 0,1 \right )$ i $\left ( 0,5 \right )$	C. $\left ( 0,1 \right )$ i $\left ( 0,-5 \right )$
B. $\left ( 1,0 \right )$ i $\left ( 5,0 \right )$	D. $\left ( 0,-1 \right )$ i $\left ( 0,5 \right )$

zadanie 28 (0-1)

Na płaszczyźnie w kartezjańskim układzie współrzędnych $\left ( x,y \right )$ , dane są proste $k$ i $l$ o równaniach

$k:y=\frac{1}{3}x-3$

$l:y=3x+6$

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Proste $k$ i $l$

A. nie mają punktów wspólnych.

B. są prostopadłe.

C. przecinają się w punkcie $P=\left ( 0,-1 \right )$ .

D. się pokrywają.

zadanie 29 (0-1)

Na płaszczyźnie w kartezjańskim układzie współrzędnych $\left ( x,y \right )$ , dane są punkty $A=\left ( 1,2 \right )$ i $B=\left ( 2m,m \right )$ , gdzie $m$ jest liczbą rzeczywistą, oraz prosta $k$ o równaniu $y=-x-1$

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Prosta przechodząca przez punkty $A$ i $B$ jest równoległa do prostej $k$ , gdy

A. $m=-1$

B. $m=1$

C. $m=\frac{1}{2}$

D. $m=2$

zadanie 30

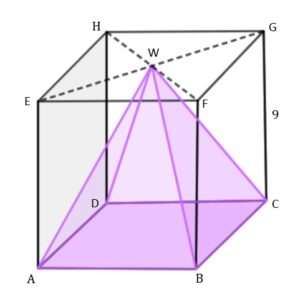
Dany jest sześcian $ABCDEFGH$ o krawędzi długości $9$ . Wierzchołki podstawy $ABCD$ sześcianu połączono odcinkami z punktem $W$ , który jest punktem przecięcie przekątnych podstawy $EFGH$ . Otrzymano w ten sposób ostrosłup prawidłowy czworokątny $ABCDW$ (zobacz rysunek)