2022 grudzień rozszerzenie

zadanie 1 (0-2)

Oblicz

$\frac{\log _{3}5\cdot \log _{25}27}{\log _{7}\sqrt[6]{49}}$

Zapisz obliczenia

zadanie 2

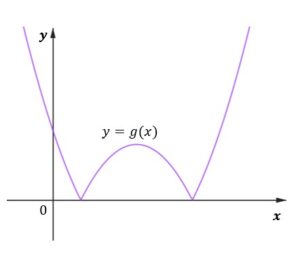Funkcja $g$ jest określona wzorem $g\left ( x \right )=\left | -\frac{1}{4}x^2 +3x-5\right |$ dla każdego $x\in \mathbb{R}$ . Fragment funkcji $g$ w kartezjańskim układzie współrzędnych $\left ( x,y \right )$ przedstawiono na rysunku (jednostki pominięto)

zadanie 2.1 (0-2)

Wyznacz zbiór wszystkich wartości jakie funkcja $g$ przyjmuje w przedziale $\left [ 9,11 \right ]$

Zapisz obliczenia

zadanie 2.2 (0-2)

Wyznacz zbiór wszystkich wartości parametru $m$ , dla których równanie $g(x)=\left | m \right |$ ma dokładnie dwa rozwiązania dodatnie.

zadanie 3 (0-3)

Wykaż, że dla każdej liczby rzeczywistej $x$ oraz dla każdej liczby rzeczywistej $y$ , spełniających warunek $x+y\geq 1$ , prawdziwa jest nierówność

$x^{3}+2xy+y^3\geq x^2+xy(x+y)+y^2$

zadanie 4 (0-3)

Maszyna napełnia torebki herbatą. Każda torebka ma zostać napełniona $200g$ herbaty. Torebkę, która zawiera mnie niż $200g$ herbaty, nazywamy torebką z niedowagą. Prawdopodobieństwo tego, że pojedyncza torebka napełniona przez tę maszynę jest z niedowagą, jest równe $0,1$ . Kontroli poddano masę herbaty w torebkach napełnianych przez tę maszynę danego dnia. Do kontroli wybrano losowo $20$ torebek.

Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wśród tych $20$ losowo wybranych torebek znajdą się co najwyżej dwie torebki z niedowagą.

Zapisz obliczenia. Wynik zapisz w zaokrągleniu do drugiego miejsca po przecinku.

zadanie 5 (0-4)

Rozwiąż równanie

$6\sin x+2\sqrt{3}\cos x+3\textup{tg}x+\sqrt{3}=0$

Zapisz obliczenia.

zadanie 6 (0-4)

W trójkącie $ABC$ poprowadzono dwusieczne kątów przecinające boki $BC,AC$ i $AB$ tego trójkąta w punktach – odpowiednio – $K,L$ oraz $M$ . Punkt $P$ jest punktem przecięcia tych dwusiecznych. Na czworokątach $CLPK$ oraz $BKPM$ można opisać okrąg.

Udowodnij, że trójkąt $ABC$ jest równoboczny.

zadanie 7 (0-4)

Olejarnia wytwarza olej ekologiczny. Aby produkcja była opłacalna, dzienna wielkość produkcji musi wynosić co najmniej $480$ litrów i nie może przekraczać $530$ litrów (ze względu na ograniczone moce produkcyjne). Przy poziomie produkcji $\left ( 480+x \right )$ litrów dziennie przeciętny koszt $K$ (w złotych) wytworzenia jednego litra oleju jest równy

$K(x)=\frac{22x^2-621,5x+23\430}{480+x}$ , gdzie $x\in \left [ 0,50 \right ]$ .

Oblicz, ile litrów oleju dziennie powinna wytworzyć olejarnia, aby przeciętny koszt produkcji jednego litra oleju był najmniejszy (z zachowaniem opłacalności produkcji).

Oblicz ten najmniejszy przeciętny koszt.

Zapisz obliczenia.

zadanie 8 (0-5)

Rozwiąż nierówność

$\frac{x-1}{x^2-4}-\frac{1}{2-x}\geq \frac{3}{2+x}+2$

Zapisz obliczenia.

zadanie 9 (0-5)

Wyznacz wszystkie wartości parametru $m$ ,dla których równanie

$x^2-\left ( m-4 \right )x+m^2-7m+12=0$

ma dwa różne rozwiązania rzeczywiste $x_{1}$ oraz $x_{2}$ , spełniające warunek

$x_{1}^{3}+x_{2}^{3}< 5x_{1}^{2}x_{2}+5x_{1}x_{2}^{2}$

Zapisz obliczenia.

zadanie 10 (0-5)

Dany jest ostrosłup prawidłowy czworokątny $ABCDS$ o podstawie $ABCD$ . Krawędź podstawy tego ostrosłupa ma długość $a$ . Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem o mierze $\alpha$ takim, że $\cos \alpha =\frac{\sqrt{10}}{10}$ . Przez krawędź $BC$ podstawy ostrosłupa poprowadzono płaszczyznę $\pi$ prostopadłą do ściany bocznej $SAD$ .

Sporządź rysunek tego ostrosłupa, zaznacz na rysunku przekrój wyznaczony przez płaszczyznę $\pi$ i nazwij figurę, która jest tym przekrojem. Oblicz pole otrzymanego przekroju.

Zapisz obliczenia.

zadanie 11 (0-5)

Dany jest trapez $ABCD$ o podstawach $AB$ i $CD$ , w którym $\left | AB \right |> \left | CD \right |$ oraz ramię $BC$ ma długość 6. Na tym trapezie opisano okrąg o promieniu $R=5$ . Miary kątów $BAC$ i $ABC$ tego trapezu spełniają warunek

$\frac{\sin \left | \measuredangle BAC\right |}{\sin \left | \measuredangle ABC \right |}=\frac{5}{8}$

Oblicz pole i obwód trapezu.

Zapisz obliczenia.

zadanie 12 (0-6)

Prosta $k$ o równaniu $x+y-9=0$ przecina parabolę o równaniu $y=\frac{1}{4}x^2-\frac{3}{2}x+\frac{1}{4}$ w punktach $A$ oraz $B$ . Pierwsza współrzędna punktu $A$ jest liczbą dodatnią; pierwsza współrzędna punktu $B$ jest liczba ujemną. Prosta $l$ jest równoległa do prostej $k$ i styczna do danej paraboli w punkcie C.

Oblicz odległość punktu $C$ od prostej $k$ oraz pole trójkąta $ABC$ .

Zapisz obliczenia.

Was this helpful?

1 / 0