zadanie 1 (0-1)
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Wartość wyrażenia |
||||
|
zadanie 2 (0-1)
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Wartość wyrażenia |
||||
|
zadanie 3 (0-1)
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Wszystkich różnych liczb naturalnych czterocyfrowych, które są nieparzyste i podzielne przez |
||||
|
zadanie 4 (0-1)
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Dla każdej liczby rzeczywistej |
||||
|
zadanie 5 (0-2)
| Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych. | ||||||
| Dla każdej liczby rzeczywistej |
||||||
|
zadanie 6 (0-3)
| Rozwiąż równanie
|
| Zapisz obliczenia. |
zadanie 7 (0-1)
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Równanie
ma w zbirze liczb rzeczywistych dokładnie |
||||
|
zadanie 8 (0-1)
| Spośród nierówności A-D wybierz tę, której zbiór wszystkich rozwiązań zaznaczono na osi liczbowej. | ||||
 |
||||
|
zadanie 9 (0-1)
| Klient banku wypłacił z bankomatu kwotę Niech |
||||
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Poprawny układ równań prowadzący do obliczenia liczb |
||||
|
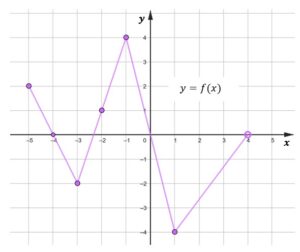
zadanie 10
|
zadanie 10.1 (0-1)
| Zapisz w wykropkowanym miejscu zbiór wartości funkcji |
| ………………………………………………………………………………………………………………………………………………………………………. |
zadanie 10.2 (0-1)
| Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F- jeśli jest fałszywe. | ||||||
|
zadanie 10.3 (0-1)
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Najmniejsza wartość funkcji |
||||
|
zadanie 11 (0-1)
| W kartezjańskim układzie współrzędnych |
||||
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Odległość punktu |
||||
|
zadanie 12
| Basen ma długość Odległość |
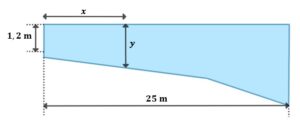 |
zadanie 12.1 (0-1)
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Największa głębokość basenu jest równa | ||||
|
zadanie 12.2 (0-2)
| Oblicz wartość współczynnika |
| Zapisz obliczenia. |
zadanie 13
| Funkcja kwadratowa |
zadanie 13.1 (0-1)
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Wykresem funkcji |
||||
|
zadanie 13.2 (0-1)
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Zbiorem wartości funkcji |
||||
|
zadanie 14
| Dany jest ciąg |
zadanie 14.1 (0-1)
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Pięćdziesiątym wyrazem ciągu |
||||
|
zadanie 14.2 (0-1)
| Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F- jeśli jest fałszywe. | ||||||
|
zadanie 15 (0-1)
| Na płaszczyźnie, w kartezjańskim układzie współrzędnych |
||||
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Współczynnik |
||||
|
zadanie 16
| Dany jest ciąg |
zadanie 16.1 (0-1)
| Dokończ zdanie, tak aby było prawdziwe. Wybierz odpowiedź A, B albo C oraz jej uzasadnienie 1., 2. albo 3. | |||||||||||||||
| Ciąg |
|||||||||||||||
|
zadanie 16.2 (0-1)
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Najmniejszą wartością |
||||
|
zadanie 16.3 (0-1)
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Suma |
||||
|
zadanie 17 (0-1)
Na płaszczyźnie, w kartezjańskim układzie współrzędnych
|
||||
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Proste |
||||
|
zadanie 18 (0-1)
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Wartość wyrażenia |
||||
|
zadanie 19 (0-1)
| W pojemniku są wyłącznie kule białe i czerwone. Stosunek liczby kul białych do liczby kul czerwonych jest równy |
||||
| C | ||||
| Prawdopodobieństwo wylosowania kuli białej jest równe | ||||
|
zadanie 20 (0-1)
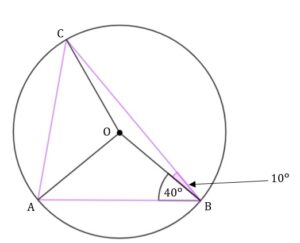
| Punkty |
||||
 |
||||
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Miara kąta |
||||
|
zadanie 21 (0-2)
| Dany jest trójkąt |
| Oblicz cosinus największego kąta tego trójkąta. |
| Zapisz obliczenia. |
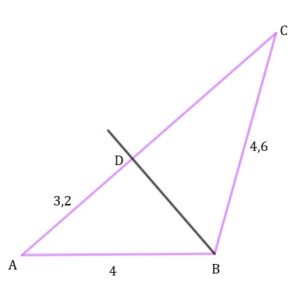
zadanie 22 (0-1)
| W trójkącie |
||||
 |
||||
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Odcinek |
||||
|
zadanie 23 (0-4)
Rodzinna firma stolarska produkuje małe wiatraki ogrodowe. Na podstawie rzeczywistych wpływów i wydatków stwierdzono, że:
Tygodniowo w zakładzie można wyprodukować co najwyżej |
| Oblicz, ile tygodniowo wiatraków należy sprzedać, aby zysk zakładu w ciągu jednego tygodnia był największy. Oblicz ten największy zysk. |
| Zapisz obliczenia. |
| Wskazówka: przyjmij, że zysk jest różnicą przychodu i kosztów. |
zadanie 24
| Firma |
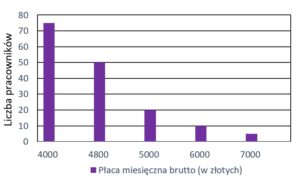 |
zadanie 24.1 (0-1)
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Średnia miesięczna płaca brutto w firmie |
||||
|
zadanie 24.2 (0-1)
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Mediana miesięcznej płacy pracowników firmy |
||||
|
zadanie 24.3 (0-1)
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Liczba pracowników firmy |
||||
|
zadanie 25 (0-3)
| Każda z krawędzi podstawy trójkątnej ostrosłupa ma długość |
| Oblicz wysokość tego ostrosłupa. |
| Zapisz obliczenia. |
zadanie 26 (0-2)
| Wykaż, że dla każdej liczby naturalnej |
Was this helpful?
0 / 1