W każdym z zadań od 1 do 28 wybierz poprawną odpowiedź.
zadanie 1 (0-1)
Liczba  jest równa jest równa |
|
|
zadanie 2 (0-1)
Liczba  jest równa jest równa |
|
|
zadanie 3 (0-1)
Liczba ^2) jest równa jest równa |
|
|
zadanie 4 (0-1)
Cenę  (w złotych) pewnego towaru obniżono najpierw o (w złotych) pewnego towaru obniżono najpierw o  , a następnie obniżono o , a następnie obniżono o  w odniesieniu do ceny obowiązującej w danym momencie. Po obydwu tych obniżkach cena towaru jest równa. w odniesieniu do ceny obowiązującej w danym momencie. Po obydwu tych obniżkach cena towaru jest równa. |
A.  złotych. złotych. |
B.  złotych. złotych. |
C.  złotych. złotych. |
D.  złotych. złotych. |
|
zadanie 5 (0-1)
Jednym z rozwiązań równania -x^2(x+1)=0) jest liczba jest liczba |
|
|
zadanie 6 (0-1)
Zbiorem wszystkich rozwiązań nierówności  jest przedział jest przedział |
|
|
zadanie 7 (0-1)
Suma wszystkich rozwiązań równania (2x-2)(x-2)=0) jest równa jest równa |
|
|
zadanie 8 (0-1)
Punkt ) należy do wykresu funkcji należy do wykresu funkcji  , określonej wzorem , określonej wzorem =\left&space;(m^2&space;-3&space;\right&space;)x^3-m^2+m+1) dla każdej liczby rzeczywistej dla każdej liczby rzeczywistej  . Wtedy . Wtedy |
|
|
zadanie 9 (0-1)
Funkcja liniowa  określona wzorem określona wzorem =\left&space;(&space;2m-5\right&space;)x+22) jest rosnąca dla jest rosnąca dla |
|
|
zadanie 10 (0-1)
Funkcja kwadratowa  określona wzorem określona wzorem =x^2+bx+c) osiąga dla osiąga dla 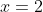 wartość najmniejszą równą wartość najmniejszą równą 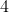 . Wtedy . Wtedy |
|
|
zadanie 11 (0-1)
Dana jest funkcja kwadratowa  określona wzorem określona wzorem =-2\left&space;(&space;x-2&space;\right&space;)\left&space;(&space;x+1&space;\right&space;)) . Funkcja . Funkcja  jest rosnąca w zbiorze jest rosnąca w zbiorze |
|
|
zadanie 12 (0-1)
Na rysunku przedstawiono wykres funkcji  określonej na zbiorze określonej na zbiorze ) . . |
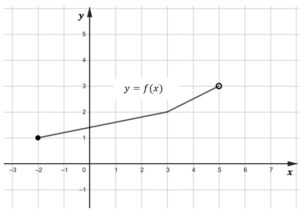 |
Funkcja 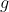 jest określona za pomocą funkcji jest określona za pomocą funkcji  następująco: następująco: =f(x-1)) . Wykres funkcji . Wykres funkcji 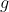 można otrzymać poprzez odpowiednie przesunięcie wykresu funkcji można otrzymać poprzez odpowiednie przesunięcie wykresu funkcji  . Dziedzina funkcji . Dziedzina funkcji 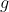 jest zbiór jest zbiór |
|
|
zadanie 13 (0-1)
Dane są ciągi  oraz oraz  , określona dla każdej liczby naturalnej , określona dla każdej liczby naturalnej 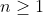 . Liczba . Liczba 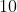 |
A. jest wyrazem ciągu ) i jest wyrazem ciągu i jest wyrazem ciągu ) . . |
B. jest wyrazem ciągu ) i nie jest wyrazem ciągu i nie jest wyrazem ciągu ) . . |
C. nie jest wyrazem ciągu ) i jest wyrazem ciągu i jest wyrazem ciągu ) . . |
D. nie jest wyrazem ciągu ) i nie jest wyrazem ciągu i nie jest wyrazem ciągu ) . . |
|
zadanie 14 (0-1)
Dany jest ciąg geometryczny ) , określony dla każdej liczby naturalnej , określony dla każdej liczby naturalnej 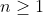 . Drugi wyraz tego ciągu oraz iloraz ciągu . Drugi wyraz tego ciągu oraz iloraz ciągu ) są równe są równe  . Suma pięciu początkowych kolejnych wyrazów tego ciągu jest równa. . Suma pięciu początkowych kolejnych wyrazów tego ciągu jest równa. |
|
|
zadanie 15 (0-1)
W ciągu dwóch godzin trzy jednakowe maszyny produkują razem 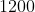 guzików. Ile guzików wyprodukuje pięć takich maszyn w ciągu jednej godziny? Przyjmij, że maszyny pracują z taką samą stałą wydajnością. guzików. Ile guzików wyprodukuje pięć takich maszyn w ciągu jednej godziny? Przyjmij, że maszyny pracują z taką samą stałą wydajnością. |
|
|
zadanie 16 (0-1)
Przyprostokątna  trójkąta prostokątnego trójkąta prostokątnego  ma długość 6, a przeciwprostokątna ma długość 6, a przeciwprostokątna  ma długość ma długość  . Wtedy tangens kąta ostrego . Wtedy tangens kąta ostrego  tego trójkąta jest równy tego trójkąta jest równy |
|
|
zadanie 17 (0-1)
Nie istnieje kąt ostry  taki, że taki, że |
|
|
zadanie 18 (0-1)
Wierzchołki 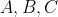 czworokąta czworokąta  leżą na okręgu o środku leżą na okręgu o środku  . Kąt . Kąt  ma miarę ma miarę  (zobacz rysunek), a przekątna (zobacz rysunek), a przekątna  jest dwusieczną tego kąta. jest dwusieczną tego kąta. |
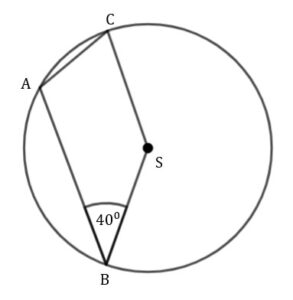 |
Miara kąta  |
|
|
zadanie 19 (0-1)
Punkty  oraz oraz  leżą na okręgu o środku leżą na okręgu o środku  . Kąt środkowy . Kąt środkowy  ma miarę ma miarę  . Prosta . Prosta 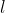 jest styczna do tego okręgu w punkcie jest styczna do tego okręgu w punkcie  i tworzy z cięciwą i tworzy z cięciwą  okręgu kąt o mierze okręgu kąt o mierze  (zobacz rysunek). (zobacz rysunek). |
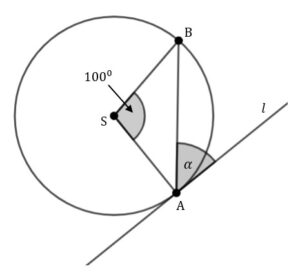 |
| Wtedy |
|
|
zadanie 20 (0-1)
Pole prostokąta jest równe 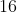 , a przekątne tego prostokąta przecinają się pod kątem ostrym , a przekątne tego prostokąta przecinają się pod kątem ostrym  , takim, że , takim, że  . Długość przekątnej tego prostokąta jest równa . Długość przekątnej tego prostokąta jest równa |
|
|
zadanie 21 (0-1)
Proste o równaniach  oraz oraz x+1) są prostopadłe, gdy są prostopadłe, gdy |
|
|
zadanie 22 (0-1)
Punkty ) oraz oraz ) są końcami przekątnej są końcami przekątnej  rombu rombu 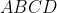 . Środek przekątnej . Środek przekątnej 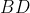 tego rombu ma współrzędne tego rombu ma współrzędne |
|
|
zadanie 23 (0-1)
Punkty ) , , ) , , ) są wierzchołkami równoległoboku są wierzchołkami równoległoboku 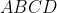 . Długość przekątnej . Długość przekątnej 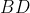 tego równoległoboku jest równa. tego równoległoboku jest równa. |
|
|
zadanie 24 (0-1)
Obrazem prostej o równaniu  w symetrii osiowej względem osi w symetrii osiowej względem osi 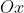 jest prosta a równaniu jest prosta a równaniu |
|
|
zadanie 25 (0-1)
W graniastosłupie prawidłowym stosunek liczby wszystkich krawędzi do liczby wszystkich ścian jest równy  . Podstawą tego ostrosłupa jest . Podstawą tego ostrosłupa jest |
| A. trójkąt. |
| B. pięciokąt. |
| C. siedmiokąt. |
| D. ośmiokąt. |
|
zadanie 26 (0-1)
Średnia arytmetyczna zestawu liczb 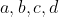 jest równa jest równa 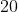 . Wtedy średnia arytmetyczna zestawu liczb . Wtedy średnia arytmetyczna zestawu liczb  jest równa jest równa |
|
|
zadanie 27 (0-1)
Wszystkich trzycyfrowych liczb naturalnych wi8ększych od 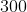 o wszystkich cyfrach parzystych jest o wszystkich cyfrach parzystych jest |
|
|
zadanie 28 (0-1)
Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ścianie ma inną liczbą oczek – od jednego do sześciu. Niech  oznacza prawdopodobieństwo otrzymania w drugim rzucie liczby oczek podzielnej przez oznacza prawdopodobieństwo otrzymania w drugim rzucie liczby oczek podzielnej przez 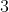 . Wtedy . Wtedy |
|
|
zadanie 29 (0-2)
| Rozwiąż nierówność |
 |
zadanie 30 (0-2)
Trójwyrazowy ciąg ) jest arytmetyczny. Suma wszystkich wyrazów tego ciągu jest równa jest arytmetyczny. Suma wszystkich wyrazów tego ciągu jest równa 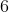 . Oblicz wszystkie wyrazy tego ciągu. . Oblicz wszystkie wyrazy tego ciągu. |
zadanie 31 (0-2)
Wykaż, że dla każdej liczby rzeczywistej  różnej od różnej od  i każdej liczby rzeczywistej i każdej liczby rzeczywistej  różnej od zera spełniona jest nierówność różnej od zera spełniona jest nierówność |
 |
zadanie 32 (0-2)
| Rozwiąż równanie |
 |
zadanie 33 (0-2)
Dany jest trójkąt równoboczny  o boku długości o boku długości 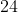 . Punkt . Punkt  leży na boku leży na boku  , a punkt , a punkt 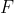 – na boku – na boku  tego trójkąta. Odcinek tego trójkąta. Odcinek 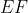 jest równoległy do boku jest równoległy do boku  i przechodzi przez środek i przechodzi przez środek  wysokości wysokości 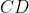 trójkąta trójkąta  (zobacz rysunek). Oblicz długość odcinka (zobacz rysunek). Oblicz długość odcinka 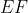 . . |
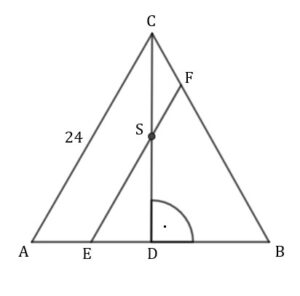 |
zadanie 34 (0-2)
Ze zbioru pięciu liczb  losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie  polega na wylosowaniu dwóch liczb, których iloczyn jest ujemny. Oblicz prawdopodobieństwo zdarzenia polega na wylosowaniu dwóch liczb, których iloczyn jest ujemny. Oblicz prawdopodobieństwo zdarzenia  . . |
zadanie 35 (0-5)