W każdym z zdań od 1. do 4. wybierz i zaznacz poprawną odpowiedź.
zadanie 1 (0-1)
Wiadomo, że  i i  . Wtedy liczba . Wtedy liczba  jest równa jest równa |
|
|
zadanie 2 (0-1)
Granica  jest równa jest równa |
|
|
zadanie 3 (0-1)
Sumą wektorów ![\vec{a}=\left [ a+2m,\frac{2}{3}n+1 \right ]](http://latex.codecogs.com/gif.latex?\vec{a}=\left&space;[&space;a+2m,\frac{2}{3}n+1&space;\right&space;]) oraz oraz ![\vec{b}=\left [ n+1,m+2 \right ]](http://latex.codecogs.com/gif.latex?\vec{b}=\left&space;[&space;n+1,m+2&space;\right&space;]) oraz wektor oraz wektor ![\vec{c}=\left [ 0,0 \right ]](http://latex.codecogs.com/gif.latex?\vec{c}=\left&space;[&space;0,0&space;\right&space;]) . Wynika stąd, że . Wynika stąd, że |
A. 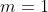 i i 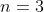 . . |
B. 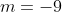 i i 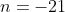 . . |
C.  i i 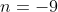 . . |
D. 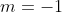 i i 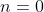 . . |
|
zadanie 4 (0-1)
Pole trójkąta ostrokątnego o bokach 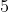 i i 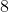 jest równe jest równe 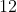 . Długość trzeciego boku tego trójkąta jest równa . Długość trzeciego boku tego trójkąta jest równa |
|
|
zadanie 5 (0-2)
Wśród  pracowników pewnej firmy jest pracowników pewnej firmy jest 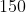 kobiet i kobiet i 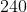 mężczyzn. Wśród nich w wieku przedemerytalnym jest mężczyzn. Wśród nich w wieku przedemerytalnym jest 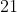 kobiet i kobiet i 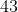 mężczyzn. Oblicz prawdopodobieństwa polegającego na tym, że losowo wybrany pracownik tej firmy w wieku przedemerytalnym – pod warunkiem, że jest mężczyzną. mężczyzn. Oblicz prawdopodobieństwa polegającego na tym, że losowo wybrany pracownik tej firmy w wieku przedemerytalnym – pod warunkiem, że jest mężczyzną. |
| W poniższe kratki wpisz kolejno – od lewej do prawej – pierwszą, drugą oraz trzecią cyfrę po przecinku nieskończonego rozwinięcia dziesiętnego otrzymanego wyniku. |
 |
zadanie 6 (0-3)
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej i dla każdej liczby rzeczywistej  takich, że takich, że 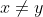 , spełniona jest nierówność , spełniona jest nierówność |
) |
zadanie 7 (0-3)
| Oblicz ile jest wszystkich liczb naturalnych pięciocyfrowych, w których zapisie występują dokładnie dwie cyfry nieparzyste. |
zadanie 8 (0-3)
| Rozwiąż nierówność |
 |
zadanie 9 (0-3)
W trapezie 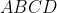 o podstawach o podstawach  i i 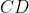 Przez punkt Przez punkt 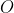 przecięcia się przekątnych poprowadzono dwie proste równoległe do boków przecięcia się przekątnych poprowadzono dwie proste równoległe do boków  i i 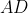 . Proste równoległa do boku . Proste równoległa do boku  przecina bok przecina bok  w punkcie w punkcie  , a prosta równoległa do boku , a prosta równoległa do boku 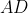 przecina bok przecina bok  w punkcie w punkcie 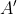 . Wykaż, że . Wykaż, że  . . |
zadanie 10 (0-4)
Dany jest nieskończony ciąg arytmetyczny ) , określony dla każdej liczby naturalnej , określony dla każdej liczby naturalnej 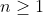 , którego iloraz , którego iloraz  jest równy pierwszemu wyrazowi i spełnia warunek jest równy pierwszemu wyrazowi i spełnia warunek  . Stosunek sumy . Stosunek sumy  wszystkich wyrazów tego ciągu o numerach nieparzystych do sumy wszystkich wyrazów tego ciągu o numerach nieparzystych do sumy 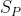 wszystkich wyrazów tego ciągu o numerach parzystych jest równy różnicy tych sum, tj. wszystkich wyrazów tego ciągu o numerach parzystych jest równy różnicy tych sum, tj.  . Oblicz . Oblicz  . . |
zadanie 11 (0-4)
Rozwiąż równanie +\sqrt{3}\sin&space;\left&space;(&space;3x&space;\right&space;)+1=0) w przedziale w przedziale ![\left [ 0,\pi \right ]](http://latex.codecogs.com/gif.latex?\left&space;[&space;0,\pi&space;\right&space;]) . . |
zadanie 12 (0-5)
Podstawą graniastosłupa prostego  jest trapez równoramienny wpisany w okrąg o środku jest trapez równoramienny wpisany w okrąg o środku 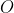 i promieniu i promieniu 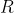 . Dłuższa podstawa . Dłuższa podstawa  trapezu jest średnicą tego okręgu, a krótsza cięciwą odpowiadającą kątowi środkowemu o mierze trapezu jest średnicą tego okręgu, a krótsza cięciwą odpowiadającą kątowi środkowemu o mierze 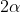 (zobacz rysunek). Przekątna ściany bocznej zawierającej ramię trapezu jest nachylona do płaszczyzny podstawy pod kątem (zobacz rysunek). Przekątna ściany bocznej zawierającej ramię trapezu jest nachylona do płaszczyzny podstawy pod kątem  . Wyznacz objętość tego graniastosłupa jako funkcję promienia . Wyznacz objętość tego graniastosłupa jako funkcję promienia 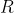 i miary kąta i miary kąta  . . |
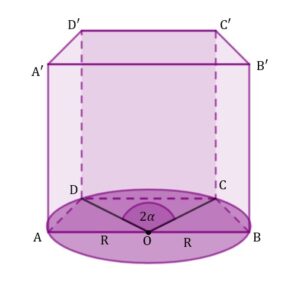 |
zadanie 13 (0-6)
Wyznacz wszystkie wartości parametru  , dla których równanie , dla których równanie |
![\left ( x-4 \right )\left [ x^2+\left ( m-3 \right )x+m^2-m-6 \right ]=0](http://latex.codecogs.com/gif.latex?\left&space;(&space;x-4&space;\right&space;)\left&space;[&space;x^2+\left&space;(&space;m-3&space;\right&space;)x+m^2-m-6&space;\right&space;]=0) |
ma trzy rozwiązania rzeczywiste 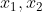 oraz oraz 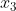 , spełniające warunek , spełniające warunek |
 |
zadanie 14 (0-6)
Dane są okrąg  o równaniu0 o równaniu0 ^{2}+\left&space;(&space;y-4&space;\right&space;)^{2}=98) oraz okrąg oraz okrąg  o promieniu o promieniu  . Środki okręgów . Środki okręgów  i i  leżą po różnych stronach prostej leżą po różnych stronach prostej  o równaniu o równaniu 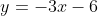 , a punkty wspólne obu okręgów leżą na prostej , a punkty wspólne obu okręgów leżą na prostej  . Wyznacz równanie okręgu . Wyznacz równanie okręgu  . . |
zadanie 15 (0-7)
Rozpatrujemy wszystkie trójkąty równoramienne ostrokątne  ) , na których opisano okrąg o promieniu , na których opisano okrąg o promieniu 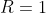 . Niech . Niech  oznacza odległość środka okręgu od podstawy oznacza odległość środka okręgu od podstawy  trójkąta. trójkąta. |
- Wykaż, że pole
 każdego z tych trójkątów, jako funkcja długości każdego z tych trójkątów, jako funkcja długości  , wyraża się wzorem , wyraża się wzorem =\left&space;(&space;x+1&space;\right&space;)\cdot&space;\sqrt{1-x^2})
- Wyznacz dziedzinę funkcji
 . .
- Oblicz długość odcinka
 tego z rozpatrywanych trójkątów, który ma największe pole. Oblicz to największe pole. tego z rozpatrywanych trójkątów, który ma największe pole. Oblicz to największe pole.
|

