W każdym z zadań od 1. do 28. wybierz i zaznacz na karcie odpowiedzi poprawna odpowiedź.
zadanie 1 (0-1)
Liczba ^{2}) jest równa jest równa |
|
|
zadanie 2 (0-1)
Dodatnie liczby  i i  spełniają warunek spełniają warunek 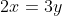 . Wynika stąd, że wartość wyrażenia . Wynika stąd, że wartość wyrażenia  jest równa jest równa |
|
|
zadanie 3 (0-1)
Liczba  jest równa jest równa |
|
|
zadanie 4 (0-1)
Cena działki po kolejnych dwóch obniżkach, za każdym razem o  w odniesieniu do ceny obowiązującej w danym momencie jest równa, w odniesieniu do ceny obowiązującej w danym momencie jest równa,  zł. Cena tej działki przed obiema obniżkami byłą, w zaokrągleniu do zł. Cena tej działki przed obiema obniżkami byłą, w zaokrągleniu do  zł równa zł równa |
|
|
zadanie 5 (0-1)
Liczba  jest równa jest równa |
|
|
zadanie 6 (0-1)
Rozwiązaniem układu równań  jest para liczb: jest para liczb: 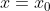 , ,  . Wtedy . Wtedy |
|
|
zadanie 7 (0-1)
Zbiorem wszystkich rozwiązań nierówności  jest przedział jest przedział |
|
|
zadanie 8 (0-1)
Iloczyn wszystkich rozwiązań równania \left&space;(&space;x+1&space;\right&space;)=0) jest równy jest równy |
|
|
zadanie 9 (0-1)
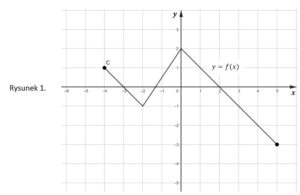
Na rysunku przedstawiono wykres funkcji  |
 |
Iloczyn \cdot&space;f(0)\cdot&space;f(4)) jest równy jest równy |
|
|
zadanie 10 (0-1)
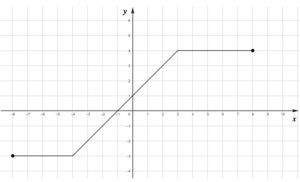
Na rysunku 1. przedstawiono wykres funkcji  określonej na zbiorze określonej na zbiorze ![\left [ -4,5 \right ]](http://latex.codecogs.com/gif.latex?\left&space;[&space;-4,5&space;\right&space;]) |
 |
Funkcję 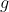 określono za pomocą funkcji określono za pomocą funkcji  . Wykres funkcji . Wykres funkcji 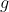 przedstawiono na rysunku 2. przedstawiono na rysunku 2. |
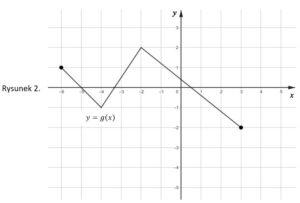 |
| Wyn9ika stąd, że |
|
|
zadanie 11 (0-1)
Miejscem zerowym funkcji liniowej  określonej wzorem określonej wzorem =-\frac{1}{3}\left&space;(&space;x+3&space;\right&space;)+5) jest liczba jest liczba |
|
|
zadanie 12 (0-1)
Wykresem funkcji kwadratowej =3x^2+bx+c) jest parabola o wierzchołku w punkcie jest parabola o wierzchołku w punkcie ) . Wzór tej funkcji w postaci kanonicznej to . Wzór tej funkcji w postaci kanonicznej to |
|
|
zadanie 13 (0-1)
Ciąg ) jest określony wzorem jest określony wzorem  dla każdej liczby naturalnej dla każdej liczby naturalnej 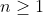 . Wtedy . Wtedy  jest równy jest równy |
|
|
zadanie 14 (0-1)
W ciągu arytmetycznym ) , określonym dla każdej liczby naturalnej , określonym dla każdej liczby naturalnej 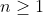 , ,  oraz oraz  . Różnica tego ciągu jest równa . Różnica tego ciągu jest równa |
|
|
zadanie 15 (0-1)
Wszystkie wyrazy nieskończonego ciągu geometrycznego ) , określonym dla każdej liczby naturalnej , określonym dla każdej liczby naturalnej 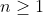 , są dodatnie i , są dodatnie i  . Wtedy iloraz tego ciągu jest równy . Wtedy iloraz tego ciągu jest równy |
|
|
zadanie 16 (0-1)
Liczba  jest równa jest równa |
|
|
zadanie 17 (0-1)
Punkty 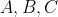 leżą na okręgu o środku leżą na okręgu o środku  . Punkt . Punkt 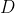 jest punktem przecięcia cięciwy jest punktem przecięcia cięciwy  i średnicy okręgu poprowadzonej z punktu i średnicy okręgu poprowadzonej z punktu  . Miara kąta . Miara kąta  jest równa jest równa  , a miara kąta , a miara kąta 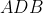 jest równa jest równa 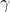 (zobacz rysunek). (zobacz rysunek). |
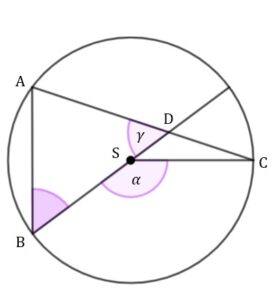 |
Wtedy kąt 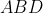 ma miarę ma miarę |
|
|
zadanie 18 (0-1)
Punkty  leżą na okręgu o środku leżą na okręgu o środku  i promieniu i promieniu 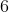 . Czworokąt . Czworokąt  jest rombem, w którym kąt ostry jest rombem, w którym kąt ostry  ma miarę ma miarę 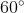 (zobacz rysunek). (zobacz rysunek). |
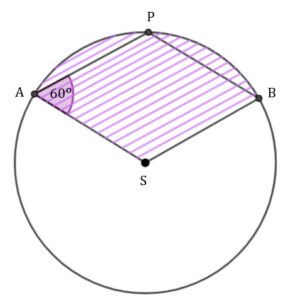 |
| Pole zakreskowanej na rysunku figury jest równe |
|
|
zadanie 19 (0-1)
Wysokość trójkąta równobocznego jest równa 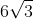 . Pole tego trójkąta jest równe . Pole tego trójkąta jest równe |
|
|
zadanie 20 (0-1)
Boki równoległoboku mają długość 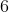 i i 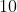 , a kąt rozwarty między tymi bokami ma miarę , a kąt rozwarty między tymi bokami ma miarę  . Pole tego równoległoboku jest równe . Pole tego równoległoboku jest równe |
|
|
zadanie 21 (0-1)
Punkty ) oraz oraz ) leżą na prostej, która przechodzi przez początek układu współrzędnych. Wtedy leżą na prostej, która przechodzi przez początek układu współrzędnych. Wtedy  jest równe jest równe |
|
|
zadanie 22 (0-1)
Dane są cztery proste  o równaniach o równaniach |
|
|
| Wśród tych prostych prostopadłe są |
A. proste  oraz oraz 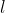 . . |
B. proste  oraz oraz  . . |
C. proste 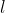 oraz oraz  . . |
D. proste  oraz oraz  . . |
|
zadanie 23 (0-1)
Punkty ) i i ) są końcami odcinka są końcami odcinka 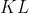 . Pierwsza współrzędna środka odcinka . Pierwsza współrzędna środka odcinka 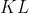 jest równa jest równa ) . Wynika stąd, że . Wynika stąd, że |
|
|
zadanie 24 (0-1)
Punkty ) i i ) są sąsiednimi wierzchołkami kwadratu są sąsiednimi wierzchołkami kwadratu 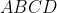 . Przekątna tego kwadratu ma długość . Przekątna tego kwadratu ma długość |
|
|
zadanie 25 (0-1)
Podstawą graniastosłupa prostego jest romb o przekątnych długości 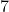 cm i cm i 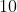 cm. Wysokość tego graniastosłupa jest krótsza od dłuższej przekątnej rombu o cm. Wysokość tego graniastosłupa jest krótsza od dłuższej przekątnej rombu o  cm. Wtedy objętość graniastosłupa jest równa cm. Wtedy objętość graniastosłupa jest równa |
|
|
zadanie 26 (0-1)
Dany jest sześcian 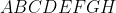 o krawędzi długości o krawędzi długości  . Punkty . Punkty  są wierzchołkami ostrosłupa są wierzchołkami ostrosłupa  (zobacz rysunek) (zobacz rysunek) |
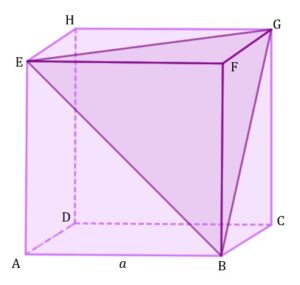 |
Pole powierzchni całkowitej ostrosłupa  jest równe jest równe |
|
|
zadanie 27 (0-1)
Wszystkich różnych liczb naturalnych czterocyfrowych nieparzystych podzielnych przez 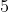 jest jest |
|
|
zadanie 28 (0-1)
Średnia arytmetyczna zestawu sześciu liczb  jest równa jest równa 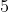 . Wynika stąd, że . Wynika stąd, że |
|
|
zadanie 29 (0-2)
| Rozwiąż nierówność |
 |
zadanie 30 (0-2)
W ciągu arytmetycznym ) , określonym dla każdej liczby naturalnej , określonym dla każdej liczby naturalnej 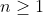 , ,  i i  . Oblicz sumę stu początkowych kolejnych wyrazów tego ciągu. . Oblicz sumę stu początkowych kolejnych wyrazów tego ciągu. |
zadanie 31 (0-2)
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej i dla każdej liczby rzeczywistej  takich, że takich, że  spełniona jest nierówność spełniona jest nierówność |
^{2}) |
zadanie 32 (0-2)
Kąt  jest ostry i jest ostry i  . Oblicz wartość wyrażenia . Oblicz wartość wyrażenia  . . |
zadanie 33 (0-2)
Dany jest trójkąt równoramienny  , w którym , w którym  . Dwusieczna kąta . Dwusieczna kąta 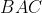 przecina bok przecina bok  w takim punkcie w takim punkcie 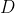 , że trójkąty , że trójkąty  i i  są podobne (zobacz rysunek). Oblicz miarę kąta są podobne (zobacz rysunek). Oblicz miarę kąta 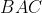 . . |
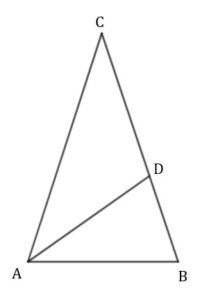 |
zadanie 34 (0-2)
Ze zbioru dziewięcioelementowego  losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie  polega na wylosowaniu dwóch liczb z zbioru polega na wylosowaniu dwóch liczb z zbioru  , których iloczyn jest równy , których iloczyn jest równy 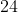 . Oblicz prawdopodobieństwo zdarzenia . Oblicz prawdopodobieństwo zdarzenia  . . |
zadanie 35 (0-5)
Wykres funkcji kwadratowej  określonej wzorem określonej wzorem =ax^2+bx+c) ma z prostą o równaniu ma z prostą o równaniu 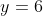 dokładnie jeden punkt wspólny. Punkty dokładnie jeden punkt wspólny. Punkty ) i i ) należą do wykresu funkcji należą do wykresu funkcji  . Oblicz wartość współczynników . Oblicz wartość współczynników 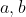 oraz oraz  . . |






