zadanie 1 (0-1)
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Wartość wyrażenia |
||||
|
zadanie 2 (0-1)
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Wartość wyrażenia |
||||
|
zadanie 3 (0-1)
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Wszystkich liczb naturalnych trzycyfrowych , w których zapisie dziesiętnym nie występuje cyfra 2 jest | ||||
|
zadanie 4 (0-1)
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Dla każdej liczby rzeczywistej |
||||
|
zadanie 5 (0-2)
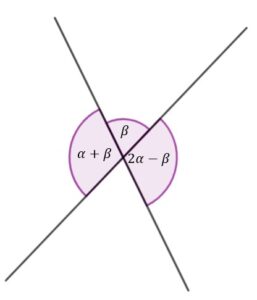
| Dane są dwie przecinające się proste. Miary kątów utworzonych przez te proste zapisano za pomocą wyrażeń algebraicznych (zobacz rysunek) | ||||||
 |
||||||
| Dokończ zdanie. Wybierz dwie odpowiedzi tak aby dla każdej z nich dokończenie poniższego zdania było prawdziwe. | ||||||
| Układem równań, w którym zapisano prawidłowe zależności między miarami kątów utworzonych przez te proste jest układ | ||||||
|
zadanie 6 (0-1)
| Dany jest wielomian | ||||
| gdzie |
||||
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Liczba |
||||
|
zadanie 7 (0-1)
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Równanie | ||||
| ma w zbiorze liczb rzeczywistych | ||||
|
zadanie 8(0-1)
| Spośród rysunków A-D, wybierz ten, na którym prawidłowo zaznaczono na osi liczbowej zbiór wszystkich liczb rzeczywistych spełniających nierówność: | ||||
|
zadanie 9 (0-2)
| Wykaż, że dla każdej liczby całkowitej nieparzystej |
zadanie 10
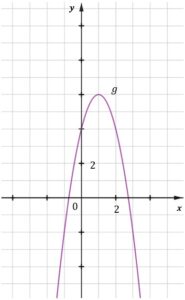
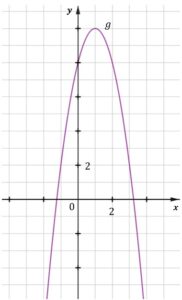
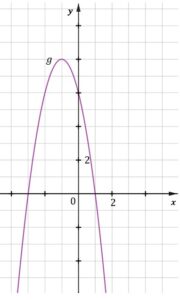
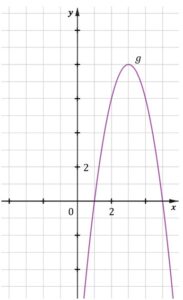
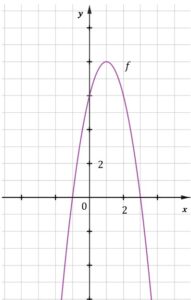
| Dana jest funkcja kwadratowa |
 |
zadanie 10.1 (0-1)
| Funkcja |
||||
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Wykres funkcji |
||||
|
zadanie 10.2 (0-1)
| Wyznacz i zapisz w miejscu wykropkowanym poniżej zbiór wszystkich rozwiązań nierówności: |
| …………………………………………………………………………………………………………………………………………………………………. |
zadnie 10.3 (0-3)
| Wyznacz wzór funkcji kwadratowej |
zadanie 11 (0-1)
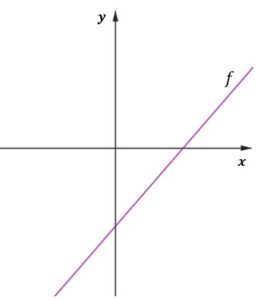
| Dana jest funkcja |
||||
 |
||||
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Współczynniki |
||||
|
zadanie 12 (0-1)
| Firma przeprowadziła badanie rynkowe dotyczące wpływu zmiany ceny |
||||
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Funkcja, która opisuje zależność liczby kupujących ten produkt od jego ceny, ma wzór | ||||
|
zadanie 13
| Czas |
| gdzie:
|
| W przypadku przyjęcia kilku(nastu) dawek powyższa zależność pozwala obliczyć, ile leku pozostało w danym momencie w organizmie z każdej poprzednio przyjętej dawki. W ten sposób obliczone masy leku z przyjętych poprzednich dawek sumują się i dają informację o całkowitej aktualnej masie leku w organizmie. |
| Pacjent otrzymuje co |
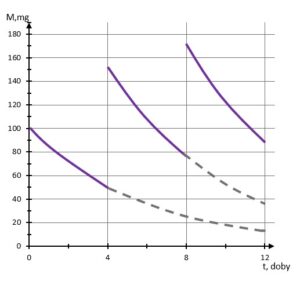
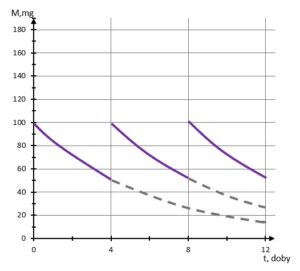
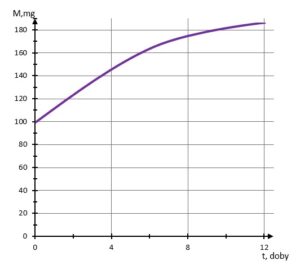
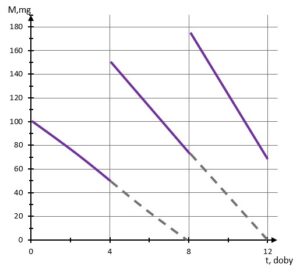
zadanie 13 (0-1)
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Wykres zależności masy |
||||
|
zadanie 13.2 (0-3)
| Oblicz masę leku |
| Zapisz obliczenia |
zadanie 14 (0-1)
| Klient wpłacił do banku |
||||
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Po |
||||
|
zadanie 15 (0-1)
| Dany jest ciąg |
||||||
| Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe. | ||||||
|
zadanie 16 (0-1)
| Dany jest trójkąt |
||||||
| Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe. | ||||||
|
zadanie 17 (0-1)
| Na płaszczyźnie w kartezjańskim układzie współrzędnych |
||||
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Równanie tego okręgu ma postać | ||||
|
||||
zadanie 18 (0-1)
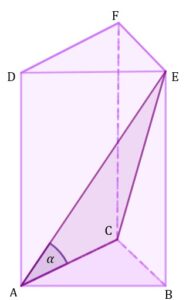
| Odcinki |
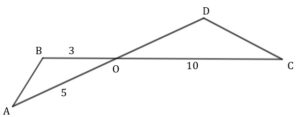 |
| Oblicz długość boku |
| Zapisz obliczenia. |
zadanie 19 (0-2)
| Na płaszczyźnie w kartezjańskim układzie współrzędnych |
||||
| Dokończ zdania. Wybierz odpowiedź spośród A-D oraz odpowiedź spośród E-H. | ||||
| 19.1. Jedną z prostych równoległych do prostej |
||||
|
||||
| 19.2. Jedną z prostych prostopadłych do prostej |
||||
|
zadanie 20 (0-1)
| W kartezjańskim układzie współrzędnych |
||||
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Długość przekątnej kwadratu |
||||
|
zadanie 21 (0-1)
| Odcinek |
||||
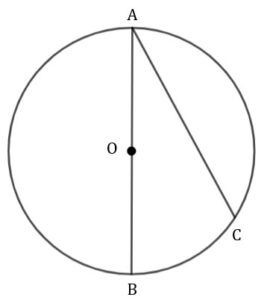 |
||||
| Dokończ zdanie. | ||||
| Wybierz właściwą odpowiedź spośród podanych. | ||||
Miara kąta
|
zadanie 22 (0-1)
| Kąt |
||||
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Tangens kąta |
||||
|
zadanie 23 (0-1)
| Dane są dwa trójkąty podobne |
|||||||||||||
| Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie 1., 2. oraz 3. | |||||||||||||
| Obwód trójkąta |
|||||||||||||
|
zadanie 24 (0-1)
| Punkty |
||||
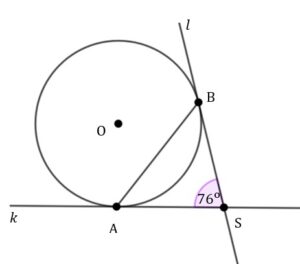 |
||||
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Miara kąta |
||||
|
zadanie 25 (0-1)
| Powierzchnię boczną graniastosłupa prawidłowego czworokątnego rozcięto wzdłuż krawędzi bocznej graniastosłupa i rozłożono na płaszczyźnie. Otrzymano w ten sposób prostokąt |
||||
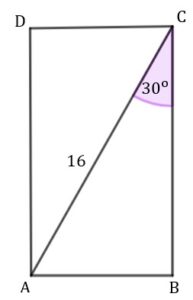 |
||||
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Długość krawędzi podstawy tego graniastosłupa jest równa | ||||
|
zadanie 26 (0-1)
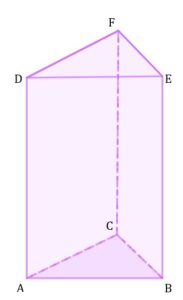
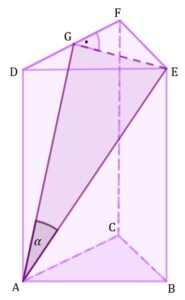
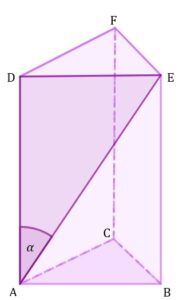
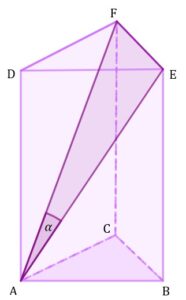
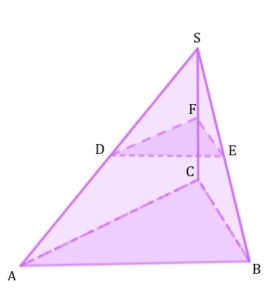
| Dany jest ostrosłup prawidłowy trójkątny |
||||
 |
||||
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Stosunek objętości ostrosłupa |
||||
|
zadanie 27 (0-1)
|
||||
|
zadanie 28 (0-3)
| W pojemniku znajdują się losy loterii fantowej ponumerowane kolejnymi liczbami naturalnymi od |
| Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że pierwszy los wyciągnięty z pojemnika był wygrywający. |
| Zapisz obliczenia. |
zadanie 29 (0-4)
| Rozważamy wszystkie równoległoboki o obwodzie równym |
| Podaj wzór i dziedzinę funkcji opisującej zależność pola takiego równoległoboku od długości |
| Oblicz wymiary tego z rozważanych równoległoboków, który ma największe pole, i oblicz to największe pole. |
| Zapisz obliczenia. |
zadanie 30
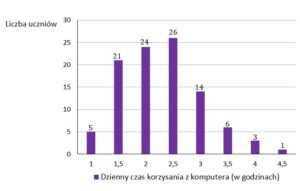
| W pewnej grupie |
 |
zadanie 30.1 (0-1)
| Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe. | ||||||
|
zadanie 30.2 (0-1)
| Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. | ||||
| Dominanta dziennego czasu korzystania przez ucznia z komputera jest równa | ||||
|
Was this helpful?
0 / 0