informator 2023 - Matma.com.pl

zadanie 1 (0-1)

Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.

Wartość wyrażenia $2021:\left ( 1-\frac{1}{2022}\right )-\left ( 1-\frac{2022}{2021} \right ):\frac{1}{2021}$ jest równa

A. $0$

B. 1

C. $2021$

D. $2023$

zadanie 2 (0-1)

Dana jest nierówność:

$\left | x-3 \right |\geq 5$

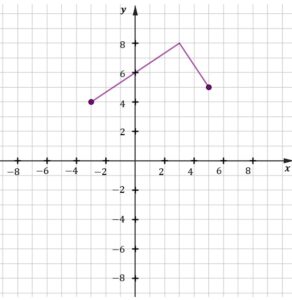
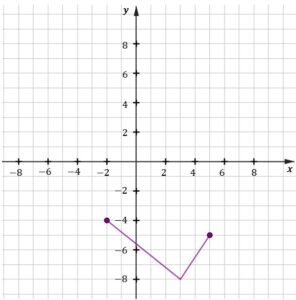
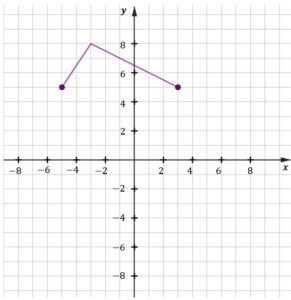
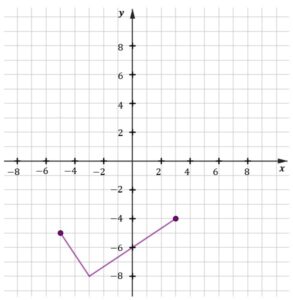
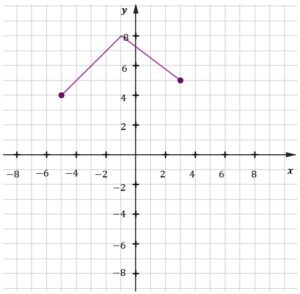
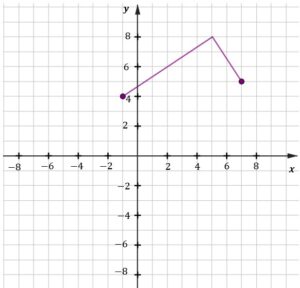
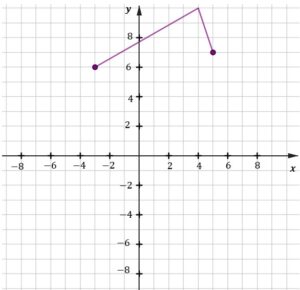
Na którym rysunku prawidłowo zaznaczono na osi liczbowej zbiór wszystkich liczb spełniających powyższą nierówność? Zaznacz właściwą odpowiedź spośród podanych.

zadanie 3 (0-1)

Oprocentowanie na długoterminowej lokacie w pewnym banku wynosi $3%$ w skali roku (już po uwzględnieniu podatków). Po każdym roku oszczędzania są doliczane odsetki od aktualnego kapitału znajdującego się na lokacie – zgodnie z procentem składanym.

Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.

Po $10$ latach oszczędzania w tym banku (i bez wypłacania kapitału ani odsetek w tym okresie) kwota na lokacie będzie większa od kwoty wpłaconej na samym początku o (w zaokrągleniu do $1%$ )

A. $30%$

B. $34%$

C. $36%$

D. $43%$

zadanie 4 (0-2)

Dane są dwie liczby $x$ i $y$ , takie, że iloraz $\frac{x}{y}$ jest równy $\frac{1+\sqrt{5}}{2}$ .

Oblicz wartość wyrażenia $\frac{x+y}{y}$ . Wynik podaj bez niewymierności w mianowniku.

zadanie 5 (0-2)

Dane są liczby $a=\sqrt{5}-2$ oraz $b=\sqrt{5}+2$ .

Oblicz wartość wyrażenia $\frac{a\cdot b}{\sqrt{a}+\sqrt{b}}:\frac{\sqrt{a}-\sqrt{b}}{a-b}$ dla podanych $a$ i $b$ .

zadanie 6 (0-2)

Dana jest liczba $a=x-\left ( \sqrt{3} -\sqrt{2}\right )^2$ , gdzie $a$ należy do zbioru $\mathbb{R}$ liczb rzeczywistych. W rozwiązaniu zadania uwzględnij fakt, że liczby $\sqrt{3}$ oraz $\sqrt{2}\cdot \sqrt{3}$ są niewymierne.

Dokończ zdanie. Zaznacz dwie odpowiedzi, tak aby dla każdej z nich dokończenie zdania było prawdziwe.

Liczba $x$ jest wymierna dla

A. $a=5$

B. $a=-\sqrt{3}+\sqrt{2}$

C. $a=\left (\sqrt{2 }-\sqrt{3} \right )^2+0,3$

D. $a=6$

E. $a=-2\sqrt{6}+12,5$

F. $a=\left (\sqrt{2 }-\sqrt{3} \right )^2-2\sqrt{6}$

G. $a=-\sqrt{6}$

zadanie 7 (0-2)

Rozwiąż równanie:

$\frac{\left ( 4x+1 \right )\left ( x-5 \right )}{\left ( 2x-10 \right )\left ( x+3 \right )}=0$

zadanie 8 (0-2)

Pensja pana $X$ jest o $50%$ wyższa od średniej krajowej, a pensja pana $Y$ jest o $40%$ niższa od średniej krajowej.

Dokończ zdania. Zaznacz odpowiedź spośród A-D oraz odpowiedź spośród E-H.

1. Pensja pana $X$ jest wyższa od pensji pana $Y$

A. o $40%$ pensji pana $Y$ .

B. o $90%$ pensji pana $Y$ .

C. o $150%$ pensji pana $Y$ .

D. o $275%$ pensji pana $Y$ .

2. Pensja pana $Y$ jest niższa od pensji pana $X$

E. o $60%$ pensji pana $X$ .

F. o $73%$ pensji pana $X$ .

G. o $90%$ pensji pana $X$ .

H. o $150%$ pensji pana $X$ .

zadanie 9 (0-1)

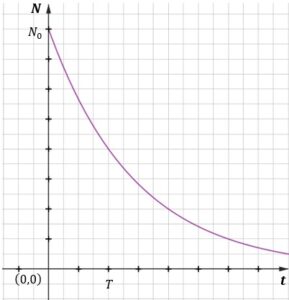
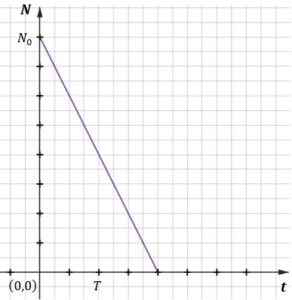
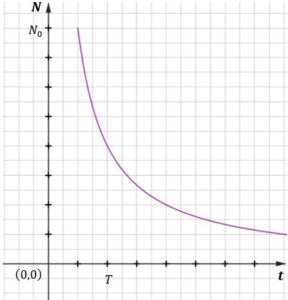
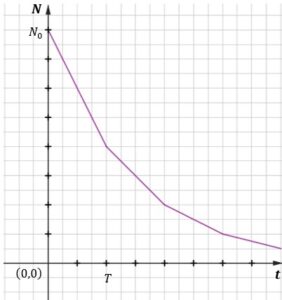
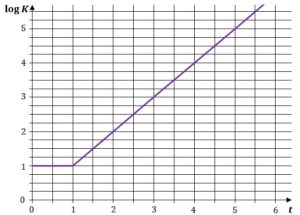
Na wykresie przedstawiono zależność $\log K(t)$ , gdzie $K(t)$ jest liczbą bakterii w próbce po czasie $t$ wyrażonym w godzinach, jaki upłynął od chwili $t=0$ rozpoczęcia obserwacji.

Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.

Gdy upłynęły dokładnie trzy godziny od chwili $t=0$ , liczba $K$ bakterii była równa

A. $3$

B. $100$

C. $1000$

D. $10000$

zadanie 10 (0-1)

Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.

Liczba $\log _{2}\left [ \left ( \sqrt{2} \right )^2\cdot \left ( \sqrt{2} \right )^4\cdot \left ( \sqrt{} \right )^8\right ]$ jest równa

A. $\sqrt{2}$

B. $7$

C. $14$

D. $2^7$

zadanie 11 (0-3)

Rozważmy takie liczby rzeczywiste $a$ i $b$ , które spełniają warunki:

$a\neq 0$ , $b\neq 0$ oraz $a^3+b^3=\left ( a+b \right )^3$

Oblicz wartość liczbową wyrażenia $\frac{a}{b}$ dla dowolnych liczb liczb rzeczywistych $a$ i $b$ , spełniających powyższe warunki.

zadanie 12 (0-1)

Dane jest wyrażenie $W(x)=\frac{1}{2}\left ( \frac{x+1}{x-1}-\frac{x-1}{x+1} \right )$ .

Oblicz prawdziwość poniższych zdań. Zaznacz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.

1.	Wartość wyrażenia $W(x)$ jest określona dla każdej liczby rzeczywistej $x\neq 1$ .	P	F
2.	Wyrażenie $W(x)$ można przekształcić równoważnie do wyrażenia $\frac{2x}{x^2-1}$ .	P	F

zadanie 13 (0-3)

Rozwiąż równanie $\left ( x-1 \right )^4-5\left ( x-1 \right )^2+6=0$

zadanie 14 (0-2)

Udowodnij, że dla każdej liczby naturalnej $n$ liczba $20n^2+30n+7=0$ przy dzieleniu przez $5$ daje resztę $2$ .

zadanie 15 (0-3)

Rozważmy dwie kolejne liczby naturalne $a$ i $b$ takie, że obie są niepodzielne przez 3.

Udowodnij, że liczba $a^3+b^3$ jest podzielna przez $9$ .

zadanie 16 (0-3)

Dany jest wielomian

$W(x)=3x^3+mx^2+3x-2$

gdzie $m$ jest pewną liczbą rzeczywistą. Wiadomo, że ten wielomian można zapisać w postaci iloczynowej:

$W(x)=\left ( x+2 \right )Q(x)$

gdzie $Q(x)$ jest pewnym trójmianem kwadratowym.

Wyznacz wielomian $Q(x)$ oraz oblicz wszystkie pierwiastki rzeczywiste wielomianu $W(x)$ .

zadanie 17 (0-1)

Dana jest funkcja $f$ określona wzorem $f(x)=x^3-b-5\sqrt{2}$ dla każdej liczby rzeczywistej $x$ .

Miejscem zerowym funkcji $f$ jest $x=\sqrt{2}+1$ .

Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.

Współczynnik $b$ we wzorze funkcji $f$ jest równy

A. $b=1$

B. $b=7$

C. $b=1-3\sqrt{2}$

D. $b=3-3\sqrt{2}$

zadanie 18 (0-1)

Funkcja kwadratowa $f$ jest określona wzorem $f(x)=3x^2+bx-5$ dla każdej liczby rzeczywistej $x$ . Współczynnik $b$ jest liczbą rzeczywista mniejszą od zera.

Dokończ zdanie. Zaznacz odpowiedź A, B albo C oraz jej uzasadnienie 1., 2. albo 3.

Funkcja $f$

ma dwa rzeczywiste miejsca zerowe,

ponieważ

$b^2+60> 0$

ma jedno rzeczywiste miejsce zerowe,

$b^2+60=0$

nie ma rzeczywistych miejsc zerowych,

$b^2+60< 0$

zadanie 19

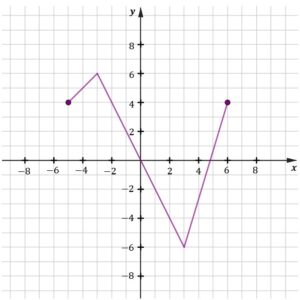Dana jest funkcja $y=f(x)$ , której wykres przedstawiono w kartezjańskim układzie współrzędnych $\left ( x,y \right )$ na rysunku obok

Ta funkcja jest określona dla każdej liczby rzeczywistej $x\in \left [ -5,8 \right ]$ .

zadanie 19.1 (0-1)

Zapisz w miejscu wykropkowanym poniżej zbiór rozwiązań nierówności:

$f(x)> 2$

………………………………………………………………………………………………………………………………………………………………………………

zadanie 19.2 (0-1)

Zapisz w miejscu wykropkowanym poniżej maksymalny przedział lub maksymalne przedziały, w których funkcja $f$ jest malejąca.

………………………………………………………………………………………………………………………………………………………………………………

zadanie 20 (0-2)

Dana jest funkcja $y=f(x)$ , której wykres przedstawiono w kartezjańskim układzie współrzędnych $\left ( x,y \right )$ na rysunku obok. Ta funkcja jest określona dla $x\in \left [ -3,5 \right ]$ . Funkcje $g$ oraz $h$ są określone za pomocą funkcji $f$ następująco:

$y=g(x)=f(x+2)$

$y=h(x)=f(-x)$

Na rysunkach A-F przedstawiono wykresy różnych funkcji – w tym wykresy funkcji $g$ oraz $h$ .

Każdej z funkcji $y=g(x)$ oraz $y=h(x)$ przyporządkuj jej wykres. Wpisz obok symboli funkcji w tabeli poniżej właściwe odpowiedzi wybrane spośród A-F.

Nr zadania	Funkcja	Rysunek
20.1
20.2

A.	B.	C.
D.	E.	F.

zadanie 21

Wzór funkcji kwadratowej można zapisać w postaci ogólnej, kanonicznej lub iloczynowej (o ile istnieje).

zadanie 21.1 (0-1)

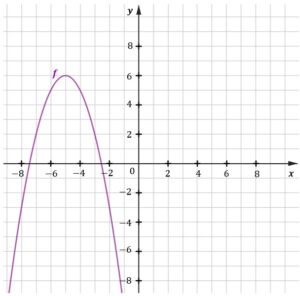Dana jest funkcja kwadratowa $y=f(x)$ , której fragment wykresu przedstawiono w kartezjańskim układzie współrzędnych $\left ( x,y \right )$ na rysunku poniżej.

Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych, jeżeli wiadomo, że jeden ze wzorów podanych w odpowiedziach A-D to wzór funkcji $f$ .

Funkcja kwadratowa $y=f(x)$ jest określona wzorem

A. $y=-(x+5)^2-6$

B. $y=-(x+5)^2+6$

C. $y=-(x-5)^2-6$

D. $y=-(x-5)^2-6$

zadanie 21.2 (0-2)

Do wykresu pewnej funkcji kwadratowej $y=g(x)$ należy punkt o współrzędnych $P=(2,-6)$ . Osią symetrii wykresu tej funkcji jest prosta o równaniu $x=3$ , a jednym z miejsc zerowych funkcji $g$ jest $x_{1}=1$ .

Wyznacz i zapisz wzór funkcji $y=g(x)$ w postaci iloczynowej.

zadanie 22

Na podstawie zasad dynamiki można udowodnić, że torem rzutu – przy pominięciu oporów powietrza jest fragment paraboli. Koszykarz wykonał rzut do kosza z odległości $x_{k}=7,01 \; \mathrm{m}$ , licząc od środka piłki do środka obręczy kosza w linii poziomej. Do opisu toru ruchu przyjmiemy układ współrzędnych, w którym środek piłki w chwili początkowej znajdował się w punkcie $x_{0}=0$ , $y_{0}=2,5\; \mathrm{m}$ . Środek piłki podczas rzutu poruszał się po paraboli danej równaniem:

$y=-0,174x^2+1,3x+2,5$

Rzut okazał się udany, a środek piłki przeszedł dokładnie przez środek kołowej obręczy kosza. Na rysunku poniżej przedstawiono tę sytuację oraz tor ruchu piłki w układzie współrzędnych.

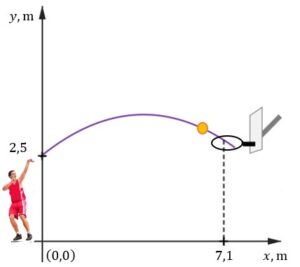zadanie 22.1 (0-1)

Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.

Obręcz kosza znajduje się na wysokości (podanej w zaokrągleniu z dokładnością do $0,01$ m)

A. $3,04\; \mathrm{m}$

B. $3,06\; \mathrm{m}$

C. $3,80\; \mathrm{m}$

D. $4,93\; \mathrm{m}$

zadanie 22.2 (0-2)

Oblicz wysokość maksymalną, na jaką wzniesie się środek piłki podczas opisanego rzutu. Zapisz wynik w zaokrągleniu do drugiego miejsca po przecinku.

zadanie 22.3 (0-3)

W opisanym rzucie piłka przeleciała swobodnie przez obręcz kosza i upadła na parkiet. Przyjmij, że obręcz kosza nie miała siatki, a na drodze rzutu nie było żadnej przeszkody. Promień piłki jest równy $0,12\; \mathrm{m}$ .

Oblicz współrzędną $x$ punktu środka piłki w momencie, w którym piłka dotknęła parkietu. Zapisz wynik w zaokrągleniu do drugiego miejsca po przecinku.

zadanie 23 (0-2)

Dany jest ciąg $\left ( a_{n} \right )$ określony wzorem rekurencyjnym:

$\left\{\begin{matrix}a_{1}=-2 & \\ a_{n+1}=n\cdot a_{n}+4& \end{matrix}\right.$ dla każdej liczby naturalnej $n\geq 1$ .

Oblicz sumę czterech początkowych wyrazów ciągu $\left ( a_{n} \right )$ .

zadanie 24 (0-2)

Dany jest ciąg $\left ( a_{n} \right )$ określony wzorem: $a_{n}=4n-9$ dla każdej liczby naturalnej $n\geq 1$ .

Wykaż, że ciąg $\left ( a_{n} \right )$ jest arytmetyczny.

zadanie 25 (0-1)

Dokończ zdanie. Zaznacz A, B albo C oraz jej uzasadnienie 1., 2. albo 3.

Ciąg $\left ( a_{n} \right )$ określony wzorem $a_{n}=n^2-n$ dla każdej liczby naturalnej $n\geq 1$ jest

A.	rosnący,		1.	różnica $a_{n+1}-a_{n}$ jest liczbą ujemną.
B.	malejący,	ponieważ dla każdej liczby naturalnej $n\geq 1$	2.	różnica $a_{n+1}-a_{n}$ jest równa zero.
C.	stały,		3.	różnica $a_{n+1}-a_{n}$ jest liczba dodatnią.

zadanie 26 (0-2)

Funkcja $f$ jest określona wzorem $f(x)=\frac{1}x{}$ dla każdej liczby rzeczywistej $x\neq 0$ .

Oblicz wartość $m$ , dla której liczby $f(m)$ , $f(1)$ , $f(2)$ są – odpowiednio – pierwszym, drugim i trzecim wyrazem ciągu geometrycznego.

zadanie 27

Czas $T$ połowicznego rozpadu izotopu promieniotwórczego to czas, po którym liczb jąder danego izotopu (a zatem i masa tego izotopu) zmniejsza się o połowę – tzn. połowa jąder danego izotopu przemienia się w inne jądra. Liczba jąder $N(t)$ izotopu promieniotwórczego pozostających w próbce po czasie $t$ , licząc od chwili $t_{0}=0$ , wyraża się zależnością wykładniczą:

$N(t)=N_{0}\left ( \frac{1}{2}\right )^{\frac{t}{T}}$

gdzie $N_{0}$ jest liczą jąder izotopu promieniotwórczego w chwili początkowej $t_{0}=0$ .

zadanie 27.1 (0-1)

Na poniższych rysunkach 1. – 4. przedstawiono wykresy różnych zależności.

Rysunek 1.	Rysunek2.
Rysunek 3.	Rysunek 4.

Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.

Wykres zależności wykładniczej $N(t)$ – opisanej we wstępie zadania – przedstawiono na

A. rysunku 1.

B. rysunku 2.

C. rysunku 3.

D. rysunku4.

zadanie 27.2 (0-3)

Czas połowicznego rozpadu węgla $_{}^{14}\textrm{C}$ to około 5700 lat. Naukowcy oszacowali za pomocą datowania radiowęglowego, że masa izotopu węgla $_{}^{14}\textrm{C}$ w pewnym organicznym znalezisku archeologicznym stanowi $\frac{1}{16}$ masy tego izotopu, jaka utrzymywała się podczas życia organizmu.

Oblicz ile lat ma opisane znalezisko archeologiczne. Wyniki podaj z dokładnością do $100$ lat.

zadanie 28 (0-4)

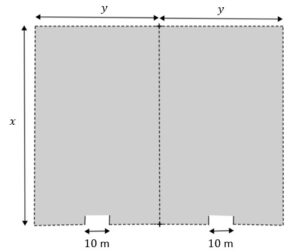Powierzchnia magazynowa będzie się składała z dwóch identycznych prostokątnych działek połączonych wspólnych bokiem. Całość ma być ogrodzona płotem, przy czym obie działki będzie rozdzielał wspólny płot. W ogrodzeniu będą zamontowane dwie bramy wjazdowe, każda o szerokości $10\; \mathrm{m}$ (zobacz rysunek poniżej). Łączna długość płatu ogradzającego oraz rozdzielającego obie działki wyniesie $580$ metrów, przy czym szerokości oby bram wjazdowych nie wliczają się w długość płotu.

Oblicz wymiary $x$ i $y$ każdej z dwóch prostokątnych działek tak aby całkowite pole powierzchni magazynowej było największe.

zadanie 29 (0-1)

Dany jest kąt o mierze $\alpha$ taki, że $\sin \alpha =\frac{4}{5}$ oraz $90^\circ <\alpha <180^\circ$ .

Oblicz prawdziwość poniższych zdań. Zaznacz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.

1.	Dla kąta $\alpha$ spełnione jest równanie: $\cos \alpha =-\frac{3}{5}$ .	P	F
2.	Dla kąta $\alpha$ spełnione jest równanie: $\left \| \mathrm{tg} \alpha \right \|=\frac{3}{4}$ .	P	F

zadanie 30 (0-2)

Oblicz długość środkowej tego trójkąta, poprowadzonej z wierzchołka $A$ .

zadanie 31 (0-4)

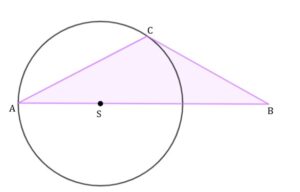Wierzchołki $A$ i $C$ trójkąta $ABC$ leżą na okręgu o promieniu $r$ . Środek $S$ tego okręgu leży na boku $AB$ tego trójkąta (zobacz rysunek poniżej). Długości boków $AB$ i $AC$ są równe odpowiednio $\left | AB \right |=3r$ oraz $\left | AC \right |=\sqrt{3}r$

Oblicz miary wszystkich kątów trójkąta $ABC$ .

zadanie 32 (0-1)

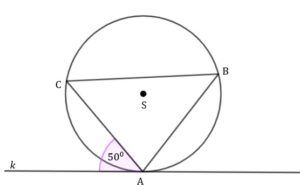Dane są okrąg o środku $S$ oraz prosta $k$ styczna do okręgu w punkcie $A$ . Odcinek $AB$ jest cięciwą tego okręgu. Miara kąta ostrego pomiędzy prostą $k$ a cięciwą $AB$ jest równa $50^\circ$ . Punkt $C$ leży na okręgu. Kąt $\measuredangle BCA$ jest ostry. Sytuacje przedstawia rysunek poniżej.

Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.

Miara kąta $\measuredangle BCA$ jest równa

A. $100^\circ$

B. $80^\circ$

C. $50^\circ$

D. $40^\circ$

zadanie 33 (0-1)

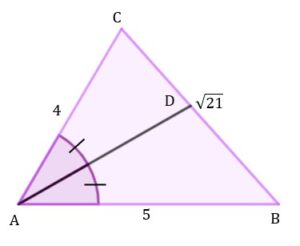Dokończ zdanie. Zaznacz odpowiedź A, B albo C oraz jej uzasadnienie 1., 2. albo 3.

Długość odcinka $BD$ jest równa

$\left | BD \right |=\frac{1}{2}\sqrt{21}$ ,

ponieważ z twierdzenia o dwusiecznej wynika, że

$\frac{\left | AB \right |}{\left | AC \right |}=\frac{\left | BC \right |}{\left | BD \right |}$

$\left | BD \right |=\frac{5}{9}\sqrt{21}$ ,

$\left | BD \right |=\left | DC \right |$

$\left | BD \right |=\frac{4}{5}\sqrt{21}$ ,

$\frac{\left | AB \right |}{\left | AC \right |}=\frac{\left | BD \right |}{\left | DC \right |}$

zadanie 34 (0-3)

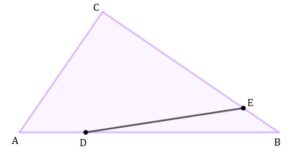Dany jest trójkąt $ABC$ . Na boku $AB$ tego trójkąta wybrano punkt $D$ , taki, że $\left | AD \right |=\frac{1}{4}\left | AB \right |$ , na boku $BC$ wybrano taki punkt $E$ , $\left | BE \right |=\frac{1}{5}\left | BC \right |$ (zobacz rysunek poniżej). Pole trójkąta $ABC$ jest równe $20$ .

Oblicz pole trójkąta $DBE$ .

zadanie 35 (0-3)

Na podstawie twierdzenia Pitagorasa można udowodnić bardziej ogólną własność niż ta, o której mówi to samo twierdzenie.

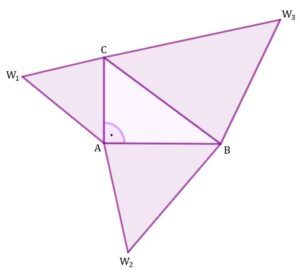Rozważmy trójkąt prostokątny $ABC$ o kącie prostym przy wierzchołku $A$ . Niech każdy z boków tego trójkąta: $CA,AB,BC$ będzie podstawą trójkątów podobnych, odpowiednio: $CAW_{1}$ , $ABW_{2}$ , $CBW_{3}$ . Trójkąty te mają odpowiadające sobie kąty o równych miarach, odpowiednio przy wierzchołkach: $W_{1},W_{2},W_{3}$ .

Pola trójkątów $CAW_{1}$ , $ABW_{2}$ , $CBW_{3}$ oznaczymy odpowiednio jako $P_{1}$ , $P_{2}$ , $P_{3}$ .

Udowodnij, że:

$P_{3}=P_{1}+P_{2}$

zadanie 36 (0-3)

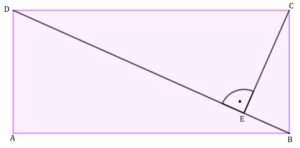Dany jest prostokąt $ABCD$ , w którym $\left | AD \right |=2$ . Kąt $BDA$ ma miarę $\alpha$ , taką, że $\mathrm{tg}\alpha =2$ . Przekątna $BD$ i prosta przechodząca przez wierzchołek $C$ prostopadła do $BD$ przecinają się w punkcie $E$ (zobacz rysunek).

Oblicz długość odcinka $\left | CE \right |$ .

zadanie 37 (0-3)

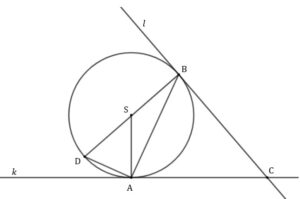Trzy różne punkty $A, B,D$ leżą na okręgu o środku w punkcie $S$ . Odcinek $BD$ jest średnicą tego okręgu. Styczne $k$ i $l$ do tego okręgu, odpowiednio w punktach $A$ i $B$ , przecinają się w punkcie $C$ (zobacz rysunek poniżej).

Wykaż, że trójkąty $ACB$ i $ASD$ są podobne.

zadanie 38 (0-3)

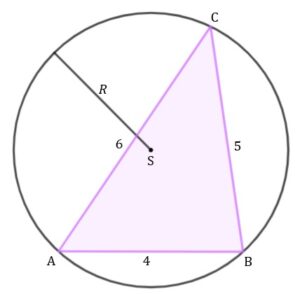Oblicz promień $R$ okręgu opisanego na trójkącie $ABC$ .

zadanie 39 (0-1)

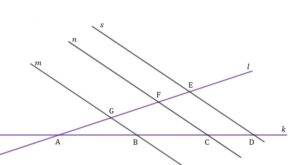Proste $k$ i $l$ przecinają się w punkcie $A$ . Proste $m,n$ i $s$ są do siebie równoległe i przecinają się obie proste $k$ i $l$ w punktach $B,C,D,E,F,G$ (zobacz rysunek poniżej), w taki sposób, że:

Oblicz długość odcinka $FE$ .

zadania 40

Na płaszczyźnie w kartezjańskim układzie współrzędnych $\left ( x,y \right )$ , dany jest okrąg $O$ określony równaniem:

$\left ( x-2 \right )^2+\left ( y+3 \right )^2=16$

zadanie 40.1 (0-1)

Dokończ zdania. Zaznacz odpowiedź spośród A-D oraz odpowiedź spośród E-G.

1. Środek $S$ okręgu $O$ ma współrzędne

A. $S=(2,-3)$

B. $S=(-2,-3)$

C. $S=(-2,3)$

D. $S=(2,3)$

2. Promień $r$ okręgu $O$ jest równy

E. $r=16$

F. $r=4$

G. $r=5$

zadanie 40.2 (0-2)

Oblicz współrzędne $x$ punktów przecięcia okręgu $O$ z osią $Ox$ .

zadanie 41

Na płaszczyźnie, w kartezjańskim układzie współrzędnych $\left ( x,y \right )$ , dany jest okrąg $O$ o środku w punkcie $S=(3,-4)$ i prosta $k$ o równaniu $2x-y-11=0$

Okrąg $O$ jest styczny do prostej $k$ w punkcie $P$ .

zadanie 41 (0-2)

Wyznacz i zapisz równanie okręgu $O$ .

zadanie 41.2 (0-2)

Oblicz współrzędne punktu $P$ , w którym okrąg $O$ jest styczny do prostej $k$ .

zadanie 42 (0-1)

Na płaszczyźnie, w kartezjańskim układzie współrzędnych $\left ( x,y \right )$ , dane są punkty $A=(1,2)$ oraz $B=(3,7)$ . Punkty $A_{0}$ oraz $B_{0}$ są odpowiednio obrazami punktów $A$ i $B$ w symetrii środkowej o środku w punkcie $O=(0,0)$ .

Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.

Współczynnik kierunkowy prostej przechodzącej przez punkty $A_{0}$ i $B_{0}$ jest równy:

A. $\frac{5}{2}$

B. $-\frac{5}{2}$

C. $\frac{2}{5}$

D. $-\frac{2}{5}$

zadanie 43

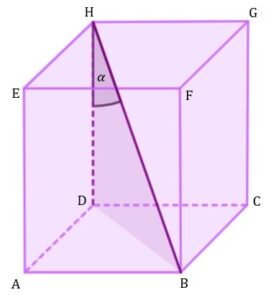
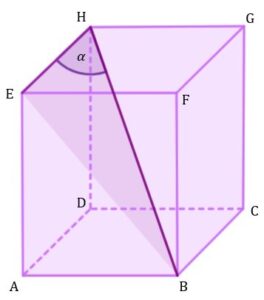
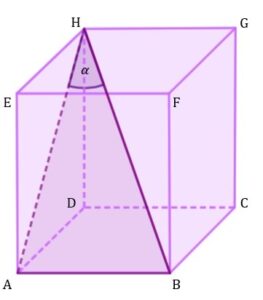
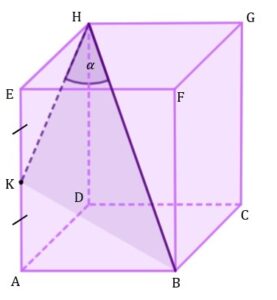
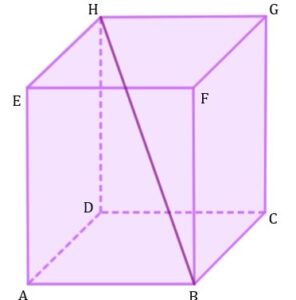Dany jest prostopadłościan $ABCDEFGH$ , w którym prostokąt $ABCD$ i $EFGH$ są jego podstawami. Odcinek $BH$ jest przekątną tego prostopadłościanu.

zadanie 43.1 (0-1)

Na którym rysunku prawidłowo narysowano, oznaczono i podpisano kąt $\alpha$ pomiędzy przekątną $BH$ prostopadłościanu a jego ścianą boczną $ADHE$ ? Zaznacz właściwą odpowiedź spośród podanych.

A. $\alpha =\measuredangle BHD$	B. $\alpha =\measuredangle BHE$
C. $\alpha =\measuredangle BHA$	D. $\alpha =\measuredangle BHK$

zadanie 43.2 (0-4)

W prostopadłościanie $ABCDEFGH$ dane są:

$\mathrm{tg}\beta =\frac{9}{7}\; \; \; \; \left | BG \right |=2\cdot \sqrt{130}\; \; \; \; \left | BH \right |=2\cdot \sqrt{194}$

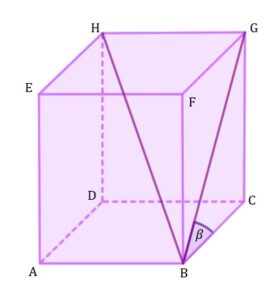gdzie odcinek $BH$ jest przekątną prostopadłościanu, odcinek $BG$ jest przekątną ściany bocznej $BCGF$ , $\beta$ jest miarą kąta $\measuredangle GBC$ . Sytuację ilustruje rysunek poniżej.

Oblicz pole powierzchni całkowitej prostopadłościanu $ABCDEFGH$ .

zadanie 44 (0-1)

Dane są dwa prostopadłościany podobne: $B_{1}$ oraz $B_{2}$ . Objętość prostopadłościanu $B_{1}$ jest równa $V$ , a objętość prostopadłościanu $B_{2}$ jest równa $27V$ . Pole powierzchni całkowitej prostopadłościanu $B_{1}$ jest równa $P$ .

Dokończ zdanie. Zaznacz odpowiedź A, B albo C oraz jej uzasadnienie 1., 2. albo 3.

Pole powierzchni całkowitej prostopadłościanu $B_{2}$ jest równe

$27P$ ,

ponieważ stosunek pól powierzchni całkowitej prostopadłościanów podobnych jest równy

stosunkowi objętości tych prostopadłościanów.

$9P$ ,

pierwiastkowi kwadratowemu ze stosunku objętości tych prostopadłościanów.

$3\sqrt{3}P$ ,

kwadratowi stosunku długości odcinków odpowiadających w obu prostopadłościanach.

zadanie 45

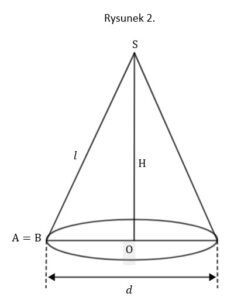
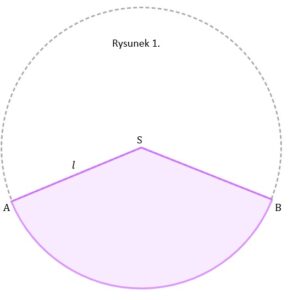
Hania zaprojektowała i wykonała czapeczkę na bal urodzinowy młodszego brata. Czapeczka miała kształt powierzchni bocznej stożka o średnicy podstawy $d=20\; cm$ , wysokości $H=25\; cm$ i tworzącej $l$ .
Żeby wykonać czapeczkę Hania najpierw wykonała na kartonie figurę płaską $ABS$ o kształcie wycinka koła o promieniu $l$ i środku $S$ (zobacz rysunek 1.). Następnie wycięła tę figurę z kartonu, odpowiednio ją wymodelowała i skleiła odcinek $SB$ z odcinkiem $SA$ (zobacz rysunek 2.).
Do obliczeń przyjmij, że rzeczywiste figury są idealne.

zadanie 45.1 (0-1)

Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.

Kąt rozwarcia stożka, którego powierzchnią boczną jest czapeczka, ma miarę (w zaokrągleniu do $1^\circ$ )

A. $44^\circ$

B. $136^\circ$

C. $22^\circ$

D. $68^\circ$

Wskazówka: skorzystaj z tablic wartości funkcji trygonometrycznych.

zadanie 45.2 (0-3)

Oblicz miarę kąta $\measuredangle BSA$ wycinka koła, z którego powstała powierzchnia boczna stożka opisanego we wstępie do zadania. Miarę kąta $\measuredangle BSA$ podaj w zaokrągleniu do jednego stopnia.

zadanie 46 (0-2)

Pojedynczy znak w piśmie Braille’a dla niewidomych jest kombinacją od 1 do 6 wypukłych punktów, które mogą zajmować miejsca ułożone w dwóch kolumnach po trzy miejsca w każdej kolumnie. Poniżej podano przykład napisu w piśmie Braille’a. Czarne kropki w znaku oznaczają wypukłości, a białe kropki oznaczają brak wypukłości. Pojedynczy znak w piśmie Braille’a musi zawierać co najmniej jeden punkt wypukły.

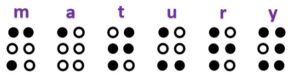Oblicz ile różnych pojedynczych znaków można zapisać w piśmie Braille’a.

zadanie 47

Andrzej ma w szafie 4 koszule: czerwoną, żółtą, zielona i niebieską; 3 pary spodni: niebieskie, czarne i szare; oraz 5 par butów: czarne, szare, zielone, czerwone i niebieskie.

Andrzej wybiera z szafy zestaw ubrania: jedną koszulę, jedną parę spodni i jedną parę butów. Zestawy ubrania wybierane przez Andrzeja określimy jako różne, gdy będą różniły się kolorem chociaż jednego rodzaju elementu ubioru w zestawie.

zadanie 47.1 (0-1)

Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.

Liczba wszystkich możliwych, różnych zestawów ubrania, jakie może wybrać Andrzej, jest równa

A. $12$

B. $72$

C. $60$

D. $720$

zadanie 47.2 (0-3)

Oblicz, na ile sposobów można wybrać taki zestaw, w którym dokładnie jeden element ubioru będzie niebieski.

zadanie 48 (0-4)

Spośród wszystkich czterocyfrowych całkowitych liczb dodatnich losujemy jedną liczbę.

Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba będzie parzysta, a w jej zapisie dziesiętnym występują dokładnie jedna cyfra 2 i dokładnie jedna cyfra 3.

zadanie 49 (0-3)

Paweł i Grzegorz postanowili zagrać w grę losową. Ich wspólny kolega będzie kolejno rzucał sześcienną symetryczną kostką do gry, której ścianki są oznaczone od $1$ do $6$ . Gdy na kostce wypadnie liczba oczek mniejsza od $4$ , to Grzegorz daje Pawłowi $10$ żetonów, a gdy na kostce wypadnie liczba oczek równa $6$ , to Paweł daje Grzegorzowi $x$ żetonów. Paweł i Grzegorz sprawiedliwie ustalili liczbę $x$ żetonów tak, aby wartość oczekiwana zysku z gry Pawła była równa wartości oczekiwanej zysku z gry Grzegorza.

Oblicz ustaloną przez Pawła i Grzegorza liczbę $x$ żetonów.

zadanie 50

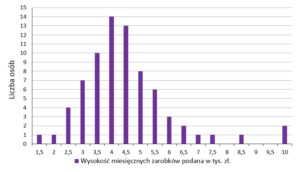
Na wykresie słupkowym poniżej podano rozkład miesięcznych zarobków wszystkich pracowników w pewnej firmie $F$ . Na osi poziomej podano – wyrażone w tysiącach złotych – miesięczne wynagrodzenie netto pracowników firmy $F$ , a na osi pionowej przedstawiono liczbę osób, która osiąga podane zarobki.

zadanie 50.1 (0-1)

Dokończ zdanie. Zaznacz odpowiedź A, B albo C oraz jej uzasadnienie 1., 2. albo 3.

Dominantą miesięcznych zarobków w firmie $F$ jest

$10$ tys. zł,

ponieważ

tę wartość zarobków osiąga najwięcej osób w firmie $F$ .

$4,5$ tys. zł,

ta wartość zarobków jest największa w firmie $F$ .

$4$ tys. zł,

iloczyn tej wartości zarobków i iloczyn liczby osób z takimi zarobkami jest największy w firmie $F$ .

zadanie 50.2 (0-1)

Uzupełnij zdanie. Wpisz odpowiednią liczbę w wykropkowanym miejscu, aby zdanie było prawdziwe.

Mediana miesięcznych zarobków w firmie $F$ jest …………………… tys. zł.

zadanie 50.3 (0-2)

Oblicz, jaki % liczby wszystkich pracowników firmy $F$ stanowią osoby zarabiające 5,5 tys. zł lub mniej.

zadanie 50.4 (0-2)

Oblicz średnią miesięcznego wynagrodzenia netto wszystkich pracowników firmy $F$ . Wynik podaj bez zaokrąglania.

Was this helpful?

0 / 0