zadanie 21 (0-3) zbiór podstawa

Wykorzystajmy wzór na prędkość aby rozwiązać to zadanie

$v=\frac{s}{t}$

Obliczmy prędkość psa oraz lisa w takim samym czasie równym $t$

Pies wykonuje dwa skoki, każdy po $2$ metry więc pokonuje drogę $4$ metrów

Prędkość psa wyraża się równanie $v_{p}=\frac{4}t{}$

lis wykonuje trzy skoki, każdy po $1$ metr więc pokonuje drogę $3$ metrów.

Prędkość lisa wyraża równanie $v_{l}=\frac{3}{t}$

Odległość między zwierzętami na początku była równa $30$ metrów.

Oznaczmy moment w którym pies dogoni lisa. Niech $T$ oznacza czas po którym to się stanie natomiast $S$ niech oznacza drogę, która zostanie pokonana do tego momentu przez oba zwierzęta.

Przekształćmy wzór na prędkość

$v=\frac{S}{T}$

$S=v\cdot T$

$T=\frac{S}{v}$

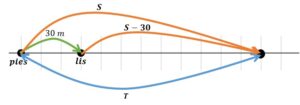
Możemy teraz zapisać czas po którym lis dostanie dogoniony przez psa

dla lisa

$T=\frac{S-30}{\frac{3}{t}}$

oraz dla psa

$T=\frac{S}{\frac{4}{t}}$

Teraz możemy porównać oba równania

$\frac{S-30}{\frac{3}{t}}=\frac{S}{\frac{4}{t}}$

$\frac{4}{t}\cdot \left ( S-30 \right )=\frac{3}{t}\cdot S$

$\frac{4S-120}{t}=\frac{3S}{t}$

$4S-120=3S$

$S=120$

Was this helpful?

0 / 0

Dodaj komentarz 0