zadanie 28 (0-2) zbiór podstawa

Zacznijmy od osi symetrii, która jest prosta o równaniu i przechodzi przez punkt $(0,4)$ na osi $OX$ .

$x=4$ jest równo oddalony od obydwu miejsc zerowych funkcji kwadratowej.

Jedno miejsce zerowe funkcji kwadratowej jest równe $x_{1}=2$ łatwo obliczymy drugie miejsce zerowe

$\frac{x_{1}+x_{2}}{2}=4\; /\cdot 2$

$2+x_{2}=8$

$x_{2}=6$

Wiemy, że funkcja kwadratowa przechodzi przez punkt $(0,8)$ . Zróbmy zatem obrazek podglądowy szukanej funkcji

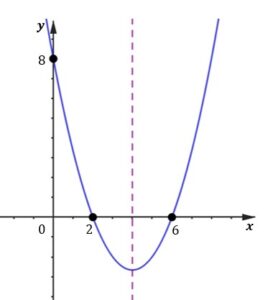
Musimy wyznaczyć postać iloczynową funkcji kwadratowej

$f(x)=a\left ( x-x_{1} \right )(x-x_{2})$

Podstawiając nasze miejsca zerowe $x_{1}=2$ i $x_{2}=6$ oraz podany punkt $(0,8)$

$8=a(0-2)(0-6)$

$8=12a\; /:12$

$a=\frac{8}{12}=\frac{2}{3}$

Ostatecznie możemy zapisać

$f(x)=\frac{2}{3}\left ( x-2 \right )\left ( x-6 \right )$

Was this helpful?

0 / 0