zadanie 37.1 (0-2) zbiór podstawa

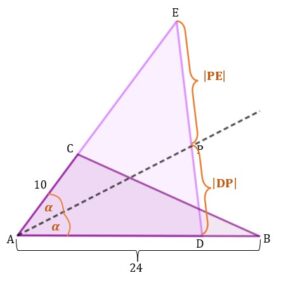
Wiemy, że $\frac{\left | DP \right |}{\left | PE \right |}=\frac{3}{4}$ , $\left | AB \right |=24$ , $\left | AC \right |=10$

oraz, że pole trójkąta $ADE$ jest dwukrotnie większe od pola trójkąta $ABC$

$2\cdot P_{\bigtriangleup ABC}=P_{\bigtriangleup ADE}$

$P_{\bigtriangleup ABC}=\frac{1}{2}\cdot \left | AB \right |\cdot \left | AC \right |\cdot \sin \left ( 2\alpha \right )$

$P_{\bigtriangleup ADE}=\frac{1}{2}\cdot \left | AD \right |\cdot \left | AE \right |\cdot \sin \left ( 2\alpha \right )$

Wracając do równania możemy zapisać:

$2\cdot \frac{1}{2}\cdot \left | AB \right |\cdot \left | AC \right |\cdot \sin \left ( 2\alpha \right )=\frac{1}{2}\cdot \left | AD \right |\cdot \left | AE \right |\cdot \sin \left ( 2\alpha \right )\; \; /\cdot 2$

Podstawiamy dane z treści zadania

$2\cdot 24\cdot 10=\left | AD \right |\cdot \left | AE \right |$

(1) $\left | AD \right |\cdot \left | AE \right |=480$

Przy pomocy twierdzeniu o dwusiecznej kąta w trójkącie:

Dwusieczna dzieli boki trójkąta $ADE$ na odcinki od długościach spełniających równanie $\frac{\left | DP \right |}{\left | PE \right |}=\frac{\left | AD \right |}{\left | AE \right |}$