zadanie 37.2 (0-3) zbiór podstawa

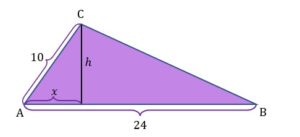
Pole trójkąta $ABC$ możemy obliczyć korzystając z wzoru:

$P_{\bigtriangleup ABC}=\frac{1}{2}\cdot \left | AB \right |\cdot h$

Z treści zadania wiemy, że pole trójkąta $ABC$ jest równe $72$ , $\left | AB \right |=24$ , $\left | AC \right |=10$

$72=\frac{1}{2\cdot}\cdot 24\cdot h$

$72=12h\: \: /:12$

$h=6$

Zastosujmy teraz dwukrotnie twierdzenie Pitagorasa

$x^2+h^2=\left | AC \right |^2$

$x^2+36=100$

$x^2=64$

$x=8$

Uzupełnijmy rysunek

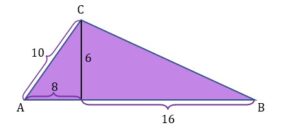
Zastosujmy jeszcze raz twierdzenie Pitagorasa

$6^2+16^2=\left | BC \right |^2$

$36+256=\left | BC \right |^2$

$\left | BC \right |^2=292$

$\left | BC \right |=\sqrt{292}$

$\left | BC \right |=2\sqrt{73}$

Was this helpful?

0 / 0