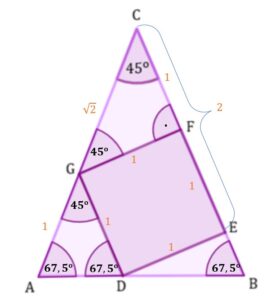
Uzupełnijmy nasz rysunek
| Zacznijmy od uzupełnienia kątów przy podstawie trójkąta równoramiennego wiemy, że pole kwadratu Widzimy, że odcinki Zajmijmy się teraz trójkątem Ostatnim etapem będzie porównanie równych boków trójkąta Możemy zatem napisać |
 |
Pierwsze zdanie jest prawdziwe.
Drugie zdanie jest prawdziwe.
Was this helpful?
0 / 0