zadanie 42 (0-3) zbiór podstawa

Oznaczmy bok kwadratu przez $x$ i $x> 0$

Pole kwadratu $ABCD$ jest równe $x^2$ .

Zauważamy, że trójkąt $SAD$ jest równoramienny i prostokątny

Uzupełnijmy rysunek

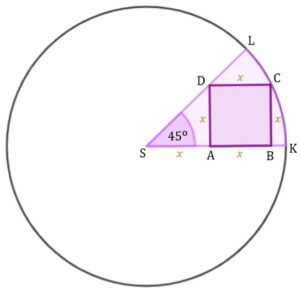
Następnie przyjrzyjmy się trójkątowi prostokątnemu $SCB$ i obliczmy promień koła korzystając z twierdzenia Pitagorasa

$\left ( 2x \right )^2+x^2=r^2$

$4x^2+x^2=r^2$

$5x^2=r^2$

$r=x\sqrt{5}$

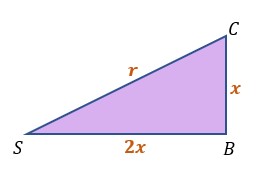Mając już promień koła możemy obliczyć pole wycinka kołowego $KSL$

${\color{Orchid} P=\frac{\alpha }{360^\circ }\cdot \pi r^2}$

$P=\frac{45^\circ }{360^\circ }\cdot \pi \cdot \left ( x\sqrt{5} \right )^2$

$P=\frac{1}{8}\cdot \pi \cdot 5x^2$

$P=\frac{5}{8}\pi x^2$

Pole kwadratu:

$P=x^2$

Pozostaje nam obliczyć stosunek pola kwadratu $ABCD$ do pola wycinka kołowego $KSL$

Mamy zatem:

$\frac{x^2}{\frac{5}{8}\pi x^2}=\frac{8}{5\pi }$

Was this helpful?

0 / 0