zadanie 43 (0-4) zbiór podstawa

Zacznijmy od trójkąta $ABD$ , który jest połową trójkąta równobocznego łatwo możemy uzupełnić jego wszystkie długości korzystając z własności trójkąta równobocznego

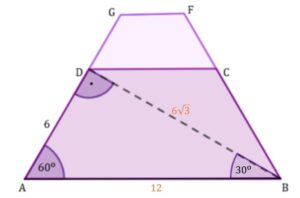
Analogicznie postąpimy aby wyznaczyć wysokość trapezu $ABCD$

$h=3\sqrt{3}$

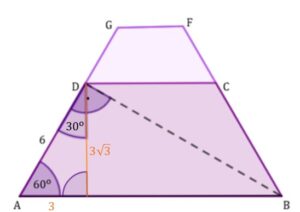
Kolejnym krokiem będzie wyznaczenie długości odcinka $\left |DC \right |=12-3-3=6$

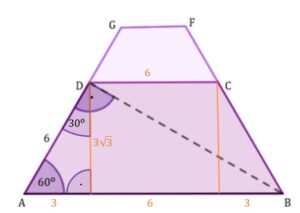
Możemy obliczyć pole trapezu $ABCD$

$P_{ABCD}=\frac{1}{2}\left ( 12+6 \right )\cdot 3\sqrt{3}$

$P_{ABCD}=\frac{1}{2}\cdot 18\cdot 3\sqrt{3}$

$P_{ABCD}=27\sqrt{3}$

Z treści zadania wiem o podobieństwie trapezu $ABCD$ oraz trapezu $DCFG$ . Szukamy skali podobieństwa porównując odpowiadające sobie boki

$k=\frac{\left | AB\right |}{\left | CD \right |}=\frac{12}{6}=2$

$k^2=4$

oznacza to że

$P_{ABCD}=k^2\cdot P_{CDFG}$

$27\sqrt{3}=4\cdot P_{CDFG}\; \; /:4$

$P_{CDFG}=\frac{27\sqrt{3}}{4}$

Was this helpful?

0 / 0