zadanie 44 (0-2) zbiór podstawa

Odcinki równoległe $b$ i $c$ podzieliły trójkąt równoboczny o boku $a$ tak, że możemy wydzielić trójkąty do niego podobne. W taki sposób możemy wyodrębnić trójkąty równoboczne jeden o boku $a$ drugi o boku $b$ i ostatni o boku $c$ .

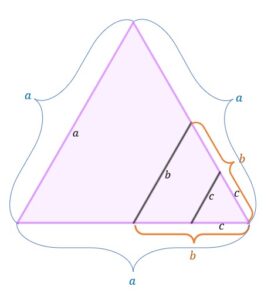
Aby obliczyć pole trapezu o podstawach $b$ i $c$ od pola trójkąta równobocznego o boku $a$ odejmiemy pole trójkąta równobocznego o boku $c$ . Mamy zatem:

$P_{T_{bc}}=\frac{a^2\sqrt{3}}{4}-\frac{c^2\sqrt{3}}{4}$

$P_{T_{bc}}=\frac{\left (a^2-c^2 \right )\sqrt{3}}{4}$

Podobnie obliczymy pole trapezu o podstawach $a$ i $b$ . Od pola trójkąta równobocznego o boku $a$ odejmiemy pole trójkąta równobocznego o boku $b$ . Otrzymujemy:

$P_{T_{ab}}=\frac{a^2\sqrt{3}}{4}-\frac{b^2\sqrt{3}}{4}$

$P_{T_{ab}}=\frac{\left (a^2-b^2 \right )\sqrt{3}}{4}$

Pozostaje nam obliczyć stosunki tych pól

$\frac{\frac{\left (a^2-c^2 \right )\sqrt{3}}{4}}{\frac{\left (a^2-b^2 \right )\sqrt{3}}{4}}=\frac{\left (a^2-c^2 \right )\sqrt{3}}{4}\cdot \frac{4}{\left ( a^2-b^2 \right )\sqrt{3}}=\frac{a^2-c^2}{a^2-b^2}$

Co należało pokazać.

Was this helpful?

0 / 0