zadanie 48 (0-4) zbiór podstawa

Zróbmy obrazek

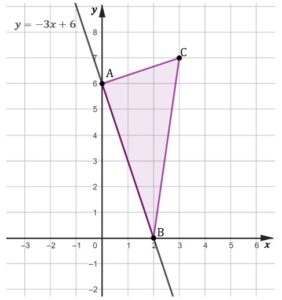
Z obrazka możemy odczytać współrzędne punktów $A=(0,6)$ oraz $B=(2,0)$ .

Możemy je również znaleźć algebraicznie posługując się równaniem prostej. I tak współrzędną $x$ punktu przecięcia prostej $y=-3x+6$ z osią $OX$ możemy obliczyć z równania

$-3x+6=0$

$-3x=-6\; \; /:(-3)$

$x=2$

Punkt $B=(2,0)$

Współrzędną $y$ punktu przecięcia prostej $y=-3x+6$ z osią $OY$ możemy obliczyć z równania

$y=-3\cdot 0+6$

$y=6$

Punkt $A=(0,6)$

Następnym krokiem będzie wyznaczenie wysokości $h$ opuszczonej z wierzchołka $C$ na odcinek $AB$ , czyli na prostą $y=-3x+6$

Obliczmy odległość punktu od prostej korzystając z wzoru:

Odległość $d$ punktu $P=(x_{0},y_{0})$ od prostej o równaniu ogólnym $Ax+By+C=0$ jest równa

${\color{Orchid} d=\frac{\left | Ax_{0} +By_{0}+C\right |}{\sqrt{A^2+B^2}}}$

Mamy zatem punkt $C=(3,7)$ oraz prostą o równaniu ogólnym $3x+y-6=0$ . Naszą odległość oznaczymy przez $h$

$h=\frac{\left | 3\cdot 3+7-6 \right |}{\sqrt{3^2+\left ( -1 \right )^2}}=\frac{\left | 9+7-6 \right |}{\sqrt{9+1}}=\frac{\left | -10 \right |}{\sqrt{10}}=\frac{10}{\sqrt{10}}\cdot \frac{\sqrt{10}}{\sqrt{10}}$