zadanie 49 (0-4) zbiór podstawa

0
0
0

Dane są punkty A=(-8,12) i B=(-2,4), które są końcami cięciwy okręgu O. Wiemy też, że środek okręgu leży na prostej o równaniu y=4x+2.

Odległość punktów A i B od środka okręgu będzie taka sama.

Oznaczmy środek okręgu S=(x_{s},y_{s}). Wiemy, że środek S leży na prostej y=4x+2 zatem możemy współrzędne punktu środka zapisać w postaci S=\left ( x_{s},4x_{s}+2 \right )

Wyznaczmy odległość punktów A od S oraz punktów B od S i je ze sobą porównajmy:

\left | AS \right |=\sqrt{\left ( x_{s}-\left ( -8 \right ) \right )^2+\left ( 4x_{s}+2-12 \right )^2}=\sqrt{\left ( x_{s}+8 \right )^2+\left ( 4x_{s}-10 \right )^2}

\left | BS \right |=\sqrt{\left ( x_{s}-\left ( -2 \right ) \right )^2+\left ( 4x_{s}+2-4 \right )^2}=\sqrt{\left ( x_{s}+2 \right )^2+\left ( 4x_{s}-2 \right )^2}

\left | AS \right |=\left | BS \right |

\sqrt{\left ( x_{s}+8 \right )^2+\left ( 4x_{s}-10 \right )^2}=\sqrt{\left ( x_{s}+2 \right )^2+\left ( 4x_{s}-2 \right )^2}

x_{s}^{2}+16x_{s}+64+16x_{s}^{2}-80x_{s}+100=x_{s}^{2}+4x_{s}+4+16x_{s}^{2}-16x_{s}+4

-64x_{s}+164=-12x_{s}+8

-52x_{s}=-156\; \; /:\left ( -52 \right )

x_{s}=3

y_{s}=4x_{s}+2

y_{s}=4\cdot 3+2

y_{s}=14

Środek okręgu ma współrzędne S=(3,14)

Pozostaje obliczyć nam długość promienia okręgu. Aby to zrobić wystarczy, że obliczymy odległość punktu A lub B od punktu S

r=\left |BS \right |=\sqrt{\left ( 3-\left ( -2 \right ) \right )^2+\left ( 14-4 \right )^2}=\sqrt{\left ( 3+2 \right )^2+10^2}=\sqrt{5^2+100}

r=\sqrt{125}=5\sqrt{5}

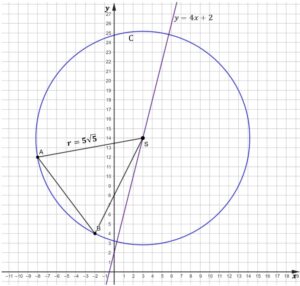
Zilustrujmy nasze zadanie

Was this helpful?

0 / 0

Dodaj komentarz 0

Your email address will not be published. Required fields are marked *