zadanie 50 (0-3) zbiór podstawa

$f(x)=-x^2+2x+3$

$g(x)=-x+5$

Zróbmy rysunek pomocniczy

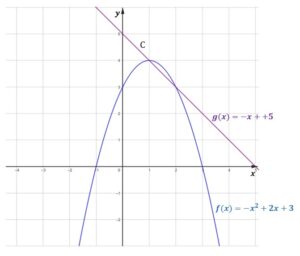
Z obrazka widzimy, że oba punkty przecięcia się wykresów funkcji znajdują się w pierwszej ćwiartce układu współrzędnych.

Wyznaczmy ich współrzędne algebraicznie. W tym celu musimy ułożyć układ równań postaci

$\left\{\begin{matrix} y=-x^2+2x+3\\ y=-x+5 \end{matrix}\right.$

$-x^2+2x+3=-x+5$

$-x^2+3x-2=0$

$\Delta =3^2-4\cdot \left ( -1 \right )\cdot \left (-2 \right )=9-8=1$

$\sqrt{\Delta }=1$

$x_{1}=\frac{-3-1}{2\cdot \left ( -1 \right )}=\frac{-4}{-2}=2$

$x_{2}=\frac{-3+1}{2\cdot \left ( -1 \right )}=\frac{-2}{-2}=1$

Dla $x_{1}=2$

$y_{1}=-2+5$

$y_{1}=3$

$\left ( x_{1},y_{1} \right )=(2,3)$

Dla $x_{2}=1$

$y_{2}=-1+5$

$y_{2}=4$

$\left ( x_{2},y_{2} \right )=(1,4)$

Szukane punkty przecięcia się wykresów funkcji $f(x)$ oraz $g(x)$ to $(2,3)$ oraz $(1,4)$ .

Was this helpful?

0 / 0

Dodaj komentarz 0