zadanie 51 (0-2) zbiór podstawa

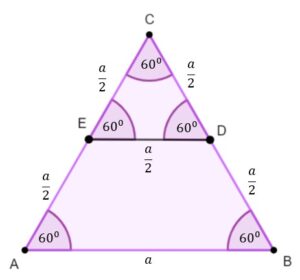
Przyjrzyjmy się podstawie naszego czworościanu

Wiemy, że wszystkie ściany czworościanu są trójkątami równobocznymi. Punkty $E$ oraz $D$ są środkami boków. Oznacza to, że $\left \| AE \right \|=\left \| EC \right \|=\left \| CD \right \|=\left \| DB\right \|=\frac{a}{2}$ . Odcinek $ED$ jest równoległy do podstawy $AB$ . Trójkąt $DCE$ jest trójkątem równobocznym o bokach długości $\frac{a}{2}$ . Zatem $\left | ED \right |=\frac{a}{2}$

Odcinki $SE$ oraz $SD$ są wysokościami ścian bocznych czworościanu o boku $a$ . Możemy zatem napisać:

$\left | SE \right |=\left | SD \right |=\frac{a\sqrt{3}}{2}$

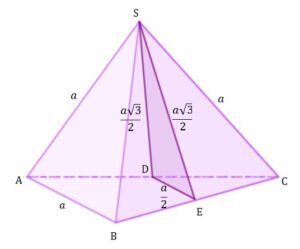Trójkąt $SED$ jest więc trójkątem równoramiennym

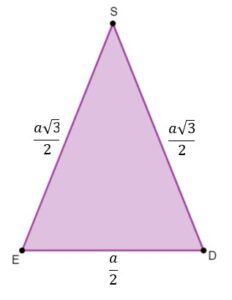
Obliczmy zatem jego wysokość korzystając z twierdzenia Pitagorasa

$h^2+\left ( \frac{a}{4} \right )^2=\left ( \frac{a\sqrt{3}}{2} \right )^2$

$h^2+\frac{a^2}{16}=\frac{3a^2}{4}$

$h^2=\frac{3a^2}{4}-\frac{a^2}{16}$

$h^2=\frac{12a^2-a^2}{16}$

$h=\frac{a\sqrt{11}}{4}$

$P_{EDS}=\frac{1}{2}\cdot \frac{a}{2}\cdot \frac{a\sqrt{11}}{4}$

$P_{EDS}=\frac{a^2\sqrt{11}}{16}$

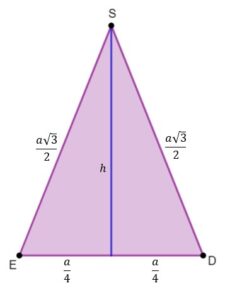Was this helpful?

0 / 0

Dodaj komentarz 0