zadanie 55 (0-1) zbiór podstawa

Uzupełnijmy nasz rysunek

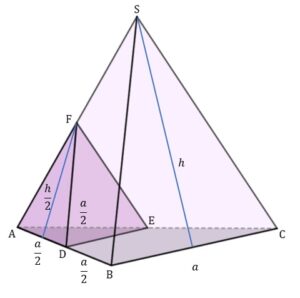Obliczmy pole powierzchni całkowitej ostrosłupa $ABCS$

$P_{C}=\frac{a^2\sqrt{3}}{4}+3\cdot \frac{1}{2}\cdot a\cdot h$

$P_{C}=\frac{a^2\sqrt{3}}{4}+ \frac{6}{4}\cdot a\cdot h$

$P_{C}=\frac{a^2\sqrt{3}+6ah}{4}$

Następnie pole powierzchni całkowitej ostrosłupa $ADEF$

$P_{C}=\frac{\left ( \frac{a}{2} \right )^2\sqrt{3}}{4}+3\cdot \frac{1}{2}\cdot \frac{a}{2}\cdot \frac{h}{2}$

$P_{C}=\frac{a^2\sqrt{3}}{16}+ \frac{3}{8}\cdot a\cdot h$

$P_{C}=\frac{a^2\sqrt{3}+6ah}{16}$

Sprawdźmy prawdziwość zdanie pierwszego:

$2\cdot \frac{a^2\sqrt{3}+6ah}{16}=\frac{a^2\sqrt{3}+6ah}{8}\neq \frac{a^2\sqrt{3}+6ah}{4}$

Pierwsze zdanie jest fałszywe.

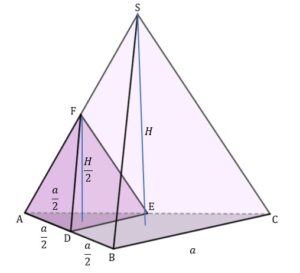Obliczmy objętość ostrosłupa $ABCS$

$V=\frac{1}{3}\cdot \frac{a^2\sqrt{3}}{4}\cdot H$

$V=\frac{a^2\sqrt{3}}{12}\cdot H$

Następnie obliczmy objętość ostrosłupa $ADEF$

$V=\frac{1}{3}\cdot \frac{\left ( \frac{a}{2} \right )^2\sqrt{3}}{4}\cdot \frac{H}{2}$

$V=\frac{1}{3}\cdot \frac{a^2\sqrt{3}}{16}\cdot \frac{H}{2}$

$V=\frac{a^2\sqrt{3}}{96}\cdot H$

Sprawdźmy prawdziwość drugiego zdania:

$8\cdot \frac{a^2\sqrt{3}}{96}\cdot H= \frac{a^2\sqrt{3}}{12}\cdot H$

Pierwsze drugie jest prawdziwe.

Was this helpful?

1 / 0