zadanie 60 (0-2) zbiór podstawa

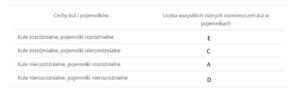
Zadanie pierwsze:

Każda kula może wpaść do jednego z dwóch pojemników. Zatem

$2\cdot 2\cdot 2\cdot 2\cdot 2=2^5$ odpowiedź E.

Zdanie drugie:

Jeśli nie rozróżniamy pojemników to oznacza, że możliwości będzie o połowę mniej niż jak w przypadku rozróżnialnych pojemników. Zatem

$\frac{2^5}{2}=2^4$ odpowiedź C.

Zdanie trzecie:

W tym przypadki kule są nierozróżnialne a pojemniki rozróżnialne czyli do pojemnika pierwszego trafi jakaś liczba kul podobnie do pojemnika drugiego. wypiszmy nasze możliwości. Możemy zapisać:

(pojemnik 1, pojemnik2)= $\left (0,5 \right ),\left ( 1,4 \right ),\left ( 2,3 \right ),\left ( 3,2 \right ),\left ( 4,1 \right ),\left ( 5,0 \right )$ . Odpowiedź A

Zdanie czwarte:

Jeśli nie rozróżniamy pojemników oraz nie rozróżniamy kul to oznacza, że będziemy mieć o połowę mniej możliwości niż w zdaniu trzecim. Zatem $\frac{6}{2}=3$ . Odpowiedź D.

Was this helpful?

1 / 0