zadanie 66 (0-3) zbiór podstawa

$f(x)=2400-15x$

$x-$ cena jednej gry

Korzystając ze wskazówki obliczmy funkcję przychodu, czyli iloczyn ceny jednostkowej ( $x$ ) gry i liczbę sprzedanych gier ( $f(x)$ ).

Funkcja przychodu ma postać

$P(x)=x\cdot f(x)$

$P(x)=x\cdot \left ( 2400-15x \right )$

$P(x)=-15x^2+2400x$

Funkcja przychodu jest funkcja kwadratową z ramionami skierowanymi do dołu ponieważ $a< 0$ ( $a=-15$ )

Narysujmy wykres (podglądowy) i znajdźmy miejsca zerowe naszej funkcji naszej funkcji

$x\left ( 2400-15x \right )=0$

$x_{1}=0\; \; \vee \; \; 2400-15x_{2}=0$

$x_{1}=0\; \; \vee \; \; 15x_{2}=2400\; \; /:15$

$x_{1}=0\; \; \vee \; \; x_{2}=160$

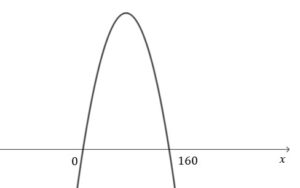Największą wartość nasza funkcja przyjmuje w punkcie odpowiadającemu wierzchołkowi paraboli

$p=\frac{0+160}{2}=80$

$q=P(p)$

$q=-15\cdot 80^2+2400\cdot 80=-15\cdot 6400+192000=-96000+129000$

$q=96000$

Zatem tygodniowy przychód $P$ będzie największy równy $96000$ gdy cena jednostkowa gry wyniesie $80$

Was this helpful?

0 / 0

Dodaj komentarz 0