zadanie 67 (0-4) zbiór podstawa

Uzupełnijmy nasz rysunek

$P_{PQRS}=6\cdot 10=60$

$P_{ABCD}=60-2\cdot \frac{1}{2}\cdot x\cdot \left ( 6-x \right )-2\cdot \frac{1}{2}\cdot x\cdot \left ( 10-x \right )$

$P_{ABCD}=60- x\cdot \left ( 6-x \right )- x\cdot \left ( 10-x \right )$

$P_{ABCD}=60-6x+ x^2-10x+x^2$

$P_{ABCD}= 2x^2-16x+60$

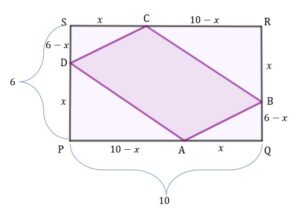Funkcja opisująca pole czworokąta $ABCD$ jest funkcją kwadratową:

$P(x)=2x^2-16x+60$

Określmy jej dziedzinę:

$x< 6\; \wedge \; x< 10\; \wedge \; x\geq 3$

Zatem $D:x\in \left [ 3,6 \right )$

Wykresem naszej funkcji jest parabola z ramionami skierowanymi ku górze.

Znajdźmy jej wierzchołek $W=\left ( p,q \right )$

$p=\frac{-\left ( -16 \right )}{2\cdot 2}=\frac{16}{4}=4$

$p\in D$

$q=P(p)$

$q=2\cdot 4^2-16\cdot 4+60=2\cdot 16-64+60=32-64+60=28$

Dla $x=4$ pole czworokąta $ABCD$ będzie najmniejsze i będzie równe $28$ .

Was this helpful?

0 / 0