zadanie 68 (0-4) zbiór podstawa

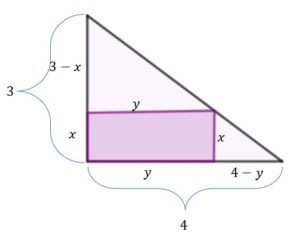
Z podobieństwa trójkątów możemy napisać, że

$\frac{3}{4}=\frac{x}{4-y}$

$3\left ( 4-y \right )=4x$

$12-3y=4x$

$-3y=4x-12\; \; /:\left ( -3 \right )$

$y=-\frac{4}{3}x+4$

Obliczmy pole prostokąta

$P=x\cdot y$

$P\left ( x \right )=x\cdot \left ( -\frac{4}{3}x+4 \right )$

$P(x)=-\frac{4}{3}x^2+4x$

Określmy dziedzinę naszej funkcji:

$x< \; \wedge \; x< 4$ oraz $x> 0$

$D:x\in \left ( 0,3 \right )$

Funkcja $P$ opisująca pole kwadratu jest parabolą z ramionami skierowanymi do dołu. Musimy obliczyć współrzędne jej wierzchołka $W=(p,q)$

$p=\frac{-4}{2\cdot \left ( -\frac{4}{3} \right )}=-4\cdot \left ( -\frac{3}{8} \right )=\frac{3}{2}$

Sprawdzamy, że $p\in D$ . Zatem pozostaje nam obliczyć największą wartość naszej funkcji kwadratowej

$q=P(p)=-\frac{4}{3}\cdot \left ( \frac{3}{2} \right )^2+4\cdot \frac{3}{2}=-\frac{4}{3}\cdot \frac{9}{4}+6=-3+6=3$

Zatem największe pole naszego prostokąta będzie równe $3$ , dla $x=\frac{3}{2}$ oraz

$y=-\frac{4}{3}\cdot \frac{3}{2}+4=-2+4=2$

Was this helpful?

0 / 0

Dodaj komentarz 0