zadanie 11 (0-4) zbiór rozszerzenie

$2x^2-\left ( 2m+7 \right )x+m^2-3m+21=0$

Równanie ma dwa różne rozwiązania rzeczywiste gdy $\Delta > 0$

$\Delta =\left ( -\left ( 2m+7 \right ) \right )^2-4\cdot 2\left ( m^2-3m+21 \right )=$

$=4m^2+28m+49-8m^2+24m-168=-4m^2+52-119$

$\Delta > 0$ zatem:

$-4m^2+52-119> 0$

$\Delta _{m}=52^2-4\cdot \left ( -4 \right )\cdot \left ( -119 \right )=2704-1904=800$

$\sqrt{\Delta _{m}}=\sqrt{800}=\sqrt{400\cdot 2}=20\sqrt{2}$

$m_{1}=\frac{-52-20\sqrt{2}}{2\cdot \left ( -4 \right )}=\frac{52+20\sqrt{2}}{8}=\frac{13+5\sqrt{2}}{2}\approx 10,04$

$m_{2}=\frac{-52+20\sqrt{2}}{2\cdot \left ( -4 \right )}=\frac{52-20\sqrt{2}}{8}=\frac{13-5\sqrt{2}}{2}\approx 2,96$

$-4m^2+52-119> 0$

$m\in \left ( \frac{13-5\sqrt{2}}{2}, \frac{13+5\sqrt{2}}{2}\right )$

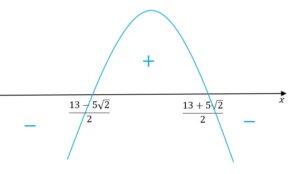Skorzystajmy teraz z wzorów Viete’a

$x_{1}+x_{2}=\frac{-b}{a}$

$x_{1}\cdot x_{2}=\frac{c}{a}$

Dla naszego równania mamy

$a=2$

$b=-2m-7$

$c=m^2-3m+21$

Zatem:

$x_{1}+x_{2}=\frac{2m+7}{2}$

$x_{1}\cdot x_{2}=\frac{m^2-3m+21}{2}$

Z treści zadania wiemy, że $x_{1}$ i $x_{2}$ spełniają warunek $x_{1}=2x_{2}$

$x_{1}+x_{2}=2x_{2}+x_{2}=3x_{2}\; \; \Rightarrow \; \; 3x_{2}=\frac{2m+7}{2}$

$x_{1}\cdot x_{2}=2x_{2}\cdot x_{2}=2x_{2}^2\; \; \Rightarrow \; \; 2x_{2}^2=\frac{m^2-3m+21}{2}\$

$\left\{\begin{matrix} 3x_{2}=\frac{2m+7}{2}\; \; /:3\\2x_{2}^2=\frac{m^2-3m+21}{2}\ \end{matrix}\right.$

$\left\{\begin{matrix} x_{2}=\frac{2m+7}{6}\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \\2\left ( \frac{2m+7}{6} \right )^2=\frac{m^2-3m+21}{2}\ \end{matrix}\right.$

$\left\{\begin{matrix} x_{2}=\frac{2m+7}{6}\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \\2\cdot \frac{4m^2+28m+49}{36} =\frac{m^2-3m+21}{2}\ \end{matrix}\right.$

$\left\{\begin{matrix} x_{2}=\frac{2m+7}{6}\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \\ \frac{4m^2+28m+49}{18} -\frac{m^2-3m+21}{2}=0\ \end{matrix}\right.$