zadanie 19 (0-3) zbiór rozszerzenie

W zadaniu musimy znaleźć długość odcinka $x$ , który odpowiada odległości punktu $O$ od podnóża wieży.

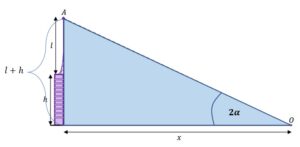Korzystając z tangensa mamy:

$\mathrm{tg}\: 2\alpha =\frac{l+h}{x}$

Z wzorów funkcji trygonometrycznym podwojonego kąta mamy:

$\mathrm{tg}\: 2\alpha =\frac{2\mathrm{tg}\, \alpha }{1-\mathrm{tg}^2\alpha }$

Przyjrzyjmy się teraz drugiemu trójkątowi prostokątnemu:

$\mathrm{tg}\, \alpha =\frac{h}{x}$

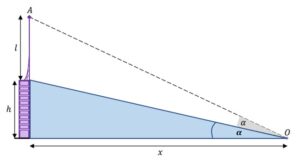Uwzględniając powyższe możemy napisać:

$\mathrm{tg}\: 2\alpha =\frac{2\mathrm{tg}\, \alpha }{1-\mathrm{tg}^2\alpha }$

$\frac{l+h}{x}=\frac{2\cdot \frac{h}{x}}{1-\left ( \frac{h}{x} \right )^2}$

$x\cdot 2\cdot \frac{h}{x}=\left ( l+h \right )\left ( 1-\frac{h^2}{x^2} \right )\; \; /:\left ( l+h \right )$

$\frac{2h}{l+h}=1-\frac{h^2}{x^2}$

$\frac{h^2}{x^2}=1-\frac{2h}{l+h}$

$\frac{h^2}{x^2}=\frac{l+h-2h}{l+h}$

$\frac{h^2}{x^2}=\frac{l-h}{l+h}$

$x^2\left ( l-h \right )=h^2\left ( l+h \right )\; \; /:\left ( l-h \right )$

$x^2=\frac{h^2\left ( l+h \right )}{l-h}$

$x=\sqrt{\frac{h^2\left ( l+h \right )}{l-h}}$

$x=h\sqrt{\frac{\left ( l+h \right )}{l-h}}$

Was this helpful?

0 / 0