zadanie 20 (0-6) zbiór rozszerzenie

Zacznijmy od uzupełnienia naszego rysunku

Najpierw obliczymy miarę kąta $OCD$ korzystając z twierdzenia o stycznej, które mówi, że styczna jest prostopadła do promienia okręgu. Mamy zatem:

$\left | \measuredangle OCD \right |=90^\circ -30^\circ =60^\circ$

Dalej obliczymy miarę kąta wpisanego w okrąg $DBC$ , która jest równa połowie kąta środkowego opisanego na tym samym łuku.

$\left | \measuredangle DBC \right |=60^\circ :2=30^\circ$

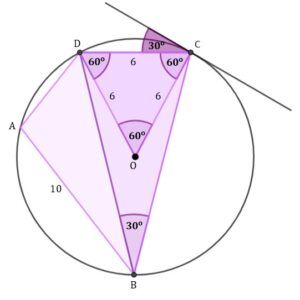Obliczmy teraz miarę kątów a trójkącie równoramiennym $ACD$ gdzie $\left | BC \right |=\left | BD \right |$

$\left | \measuredangle BCD \right |=\left | \measuredangle CDB \right |=\frac{180^\circ -30^\circ }{2}=\frac{150^\circ }{2}=75^\circ$

Następnie obliczymy miarę kąta $DAB$ korzystając z twierdzenia o okręgu opisanym na czworokącie.

Zatem

$75^\circ +\left | \measuredangle DAB \right |=180^\circ$

$\left | \measuredangle DAB \right |=105^\circ$

Teraz skorzystamy z twierdzenia sinusów aby obliczyć długość boku $BD$ . Możemy zapisać zatem:

$\frac{\left | BD \right |}{\sin 105^\circ }=2\cdot 6$

$\left | BD \right |=12\cdot \sin 105^\circ$

$\left | BD \right |=12\cdot \sin \left (45^\circ+60^\circ \right )$

$\left | BD \right |=12\cdot \left ( \sin 45^\circ \cos 60^\circ +\cos 45^\circ \sin 60^\circ \right )$

$\left | BD \right |=12\cdot \left ( \frac{\sqrt{2}}{2}\cdot \frac{\sqrt{3}}{2} +\frac{\sqrt{2}}{2}\cdot \frac{1}{2}\right )$

$\left | BD \right |=12\cdot \left (\frac{ \sqrt{6} }{4}+\frac{\sqrt{2}}{4}\right )$

$\left | BD \right |=3\sqrt{6}+3\sqrt{2}$

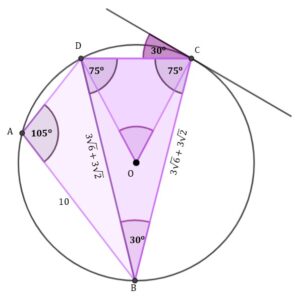Mając dany długość boku $BD$ i pamiętając, że $\left | BC \right |=\left | BD \right |$ oraz miarę kąta możemy obliczyć pole trójkąta $BCD$

$P_{\bigtriangleup BCD}=\frac{1}{2}\left ( 3\sqrt{6}+3\sqrt{2} \right )\left ( 3\sqrt{6}+3\sqrt{2} \right )\cdot \sin 30^\circ$

$P_{\bigtriangleup BCD}=\frac{1}{2}\left ( 9\cdot 6+18\sqrt{12}+9\cdot 2 \right )\cdot \frac{1}{2}$

$P_{\bigtriangleup BCD}=\frac{1}{4}\left (54+18\sqrt{4\cdot 3}+18 \right )$

$P_{\bigtriangleup BCD}=\frac{1}{4}\left (72+36\sqrt{3} \right )$

$P_{\bigtriangleup BCD}=18+9\sqrt{3}$

Zajmijmy się teraz trójkątem $ABD$ . Znajdziemy miarę kąta $ABD$

Z twierdzenia sinusów mamy:

$\frac{10}{\sin \alpha }=2\cdot 6$

$\sin \alpha =\frac{10}{12}$

$\sin \alpha =\frac{5}{6}$

$\sin ^2=\frac{25}{36}$

Z jedynki trygonometrycznej mamy

$\cos ^2\alpha =1-\frac{25}{36}$

$\cos ^2\alpha =\frac{11}{36}$

$\cos \alpha =\frac{\sqrt{11}}{6}$

Z trójkąta $ABD$ możemy napisać

$\alpha +\beta +105^\circ =180^\circ$

$\alpha +\beta =75^\circ$

$\beta =75^\circ -\alpha$

Możemy dalej napisać:

$\sin \beta =\sin \left ( 75^\circ -\alpha \right )=\sin 75^\circ\cos \alpha -\cos 75^\circ \sin \alpha$

$\sin \beta =\sin \left ( 45^\circ +30^\circ \right )\cdot \frac{\sqrt{11}}{6}-\cos \left ( 45^\circ +30^\circ \right )\cdot \frac{5}{6}$

$\sin \beta =\left (\sin 45^\circ \cos 30^\circ +\sin 30^\circ \cos 45^\circ \right ) \cdot \frac{\sqrt{11}}{6}-$

$-\left (\cos 45^\circ \cos 30^\circ -\sin 30^\circ \sin 45^\circ \right )\cdot \frac{5}{6}$

$\sin \beta =\left (\frac{\sqrt{2}}{2}\cdot \frac{\sqrt{3}}{2}+\frac{1}{2}\cdot \frac{\sqrt{2}}{2} \right )\cdot \frac{\sqrt{11}}{6}-\left ( \frac{\sqrt{2}}{2}\cdot \frac{\sqrt{3}}{2} -\frac{1}{2}\cdot \frac{\sqrt{2}}2{}\right )\cdot \frac{5}{6}$

$\sin \beta =\frac{\sqrt{6}+\sqrt{2}}{4}\cdot \frac{\sqrt{11}}{6}-\frac{\sqrt{6}-\sqrt{2}}{4}\cdot \frac{5}{6}$

$\sin \beta =\frac{\sqrt{66}+\sqrt{22}-5\sqrt{6}+5\sqrt{2}}{24}$

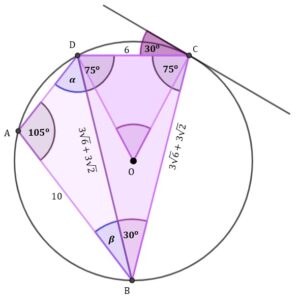Obliczmy zatem pole trójkąta $ABD$ :

$P_{\bigtriangleup ABD}=\frac{1}{2}\cdot 10\cdot \left ( 3\sqrt{6}+3\sqrt{2} \right )\cdot \sin \beta$

$P_{\bigtriangleup ABD}=5\cdot \left ( 3\sqrt{6}+3\sqrt{2} \right )\cdot \frac{\sqrt{66}+\sqrt{22}-5\sqrt{6}+5\sqrt{2}}{24}$

$P_{\bigtriangleup ABD}=5\cdot3\cdot \left ( \sqrt{6}+\sqrt{2} \right )\cdot \frac{\sqrt{66}+\sqrt{22}-5\sqrt{6}+5\sqrt{2}}{24}$

$P_{\bigtriangleup ABD}=5\cdot \left ( \sqrt{6}+\sqrt{2} \right )\cdot \frac{\sqrt{66}+\sqrt{22}-5\sqrt{6}+5\sqrt{2}}{8}$

$P_{\bigtriangleup ABD}=\frac{5\left ( \sqrt{396} +\sqrt{132}-5\cdot 6+5\sqrt{12}+\sqrt{132}+\sqrt{44}-5\sqrt{12}+5\cdot 2\right )}{8}$

$P_{\bigtriangleup ABD}=\frac{5\left ( 6\sqrt{11} +2\sqrt{132}-30+2\sqrt{11}+10\right )}{8}$

$P_{\bigtriangleup ABD}=\frac{5\left ( 8\sqrt{11} +4\sqrt{33}-20\right )}{8}$

$P_{\bigtriangleup ABD}=\frac{40\sqrt{11} +20\sqrt{33}-100}{8}$

$P_{\bigtriangleup ABD}=\frac{10\sqrt{11} +5\sqrt{33}-25}{2}$

Ostatecznie aby obliczyć pole czworokąta $ABCD$ musimy dodać do siebie pole trójkąta $ABD$ oraz pole trójkąta $BCD$ . Otrzymujemy zatem

$P_{\bigtriangleup ABD}+P_{\bigtriangleup BCD}=\frac{10\sqrt{11} +5\sqrt{33}-25}{2}+18+9\sqrt{3}$

$P_{\bigtriangleup ABD}+P_{\bigtriangleup BCD}=\frac{10\sqrt{11} +5\sqrt{33}-25}{2}+\frac{36+18\sqrt{3}}{2}$

$P_{\bigtriangleup ABD}+P_{\bigtriangleup BCD}=\frac{10\sqrt{11} +5\sqrt{33}+18\sqrt{3}+11}{2}$

Was this helpful?

2 / 0