zadanie 21 (0-4) zbiór rozszerzenie

Zaczniemy od rysunku pomocniczego

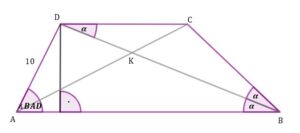Wiemy, że odcinek $BD$ jest dwusieczną kąta $ABC$ . Zatem $\left |\measuredangle ABD \right |=\left | \measuredangle DBC \right |=\alpha$

Skoro odcinki $AB$ i $DC$ są równoległe zatem $\left | \measuredangle BDC \right |=\alpha$ ponieważ jest to kąt naprzemianległy do $\left | \measuredangle ABD \right |=\alpha$ .

Możemy zatem napisać dalej że trójkąt $BCD$ jest równoramienny, w którym $\left | BC \right |=\left | CD \right |$

Uzupełnijmy nasz rysunek uwzględniając $\left | CK \right |:\left | KA \right |=1:3$ oraz oznaczymy wysokość trapezu

Skorzystamy teraz z sinusa kąta przy wierzchołku $A$

$\sin \measuredangle BAD=\frac{h}{10}$

Z treści zadania wiemy, że

$\sin \measuredangle BAD=\frac{\sqrt{6}+\sqrt{2}}{4}$

Możemy zatem zapisać:

$\frac{h}{10}=\frac{\sqrt{6}+\sqrt{2}}{4}$

$4h=10\left ( \sqrt{6}+\sqrt{2} \right )\; \; /:4$

$h=\frac{5\left ( \sqrt{6}+\sqrt{2} \right )}{2}$

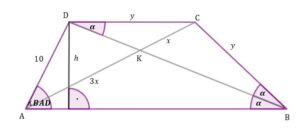Skorzystamy teraz z twierdzenia o dwusiecznej kąta w trójkącie $ABC$ . Możemy zapisać:

$\frac{\left | CK \right |}{\left | AK \right |}=\frac{\left | CB \right |}{\left | AB \right |}\; \; \Rightarrow \; \; \frac{x}{3x}=\frac{y}{\left | AB \right |}\: \: \Rightarrow \; \; \left | AB \right |=3y$