zadanie 22 (0-6) zbiór rozszerzenie

Zauważmy, że trójkąty $ABC,AMN,KBL$ i $KMD$ są podobne.

Wiemy, że Stosunek obwodu trójkąta $KMD$ do obwodu trójkąta $KBL$ jest równy $5:7$ oraz, że stosunek obwodu trójkąta $KMD$ do obwodu trójkąta $AMN$ jest równy $5:8$ .

Możemy zapisać zatem:

$\frac{x}{x+\left | MB \right |}=\frac{5}{7}$

$5x+5\left | MB \right |=7x$

$5\left | MB \right |=2x$

$\left | MB \right |=\frac{2}{5}x$

$\frac{y}{\left | BL \right |}=\frac{5}{7}$

$5\left | BL \right |=7y$

$\left | BL \right |=\frac{7}{5}y$

Analogicznie

$\frac{x}{x+\left | AK \right |}=\frac{5}{8}$

$5x+5\left | AK \right |=8x$

$5\left | AK \right |=3x$

$\left | AK \right |=\frac{3}{5}x$

$\frac{z}{\left | AN \right |}=\frac{5}{8}$

$5\left | AN \right |=8z$

$\left | AN \right |=\frac{8}{5}z$

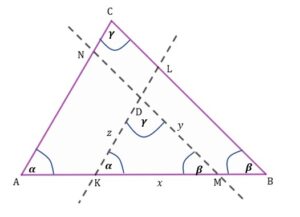Obliczmy długość boku $AB$

$\left | AB \right |=\frac{3}{5}x+x+\frac{2}{5}x=2x$

Zatem trójkąt $ABC$ jest dwa razy większy od trójkąta $KMD$ .

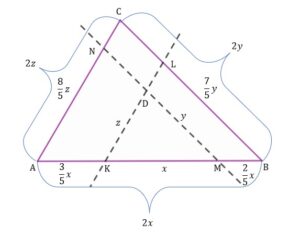Obliczymy teraz długości boków $CL$ i $NC$ .

$\left | CL \right |=2y-\frac{7}{5}y=\frac{3}{5}y$

$\left | DN \right |=\frac{3}{5}y$

$\left | NC \right |=2z-\frac{8}{5}y=\frac{2}{5}z$

$\left | NC \right |=\frac{2}{5}z$

Poprowadzimy teraz prostą prostopadłą do odcinka $AB$ i przechodzącą przez punkt $D$ . W ten sposób otrzymamy dwa trójkąty podobne do trójkąta $ABC$ .

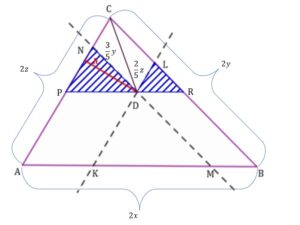Poprowadziliśmy jednocześnie odcinek $CD$ , który jest przekątną równoległoboku $DLCN$ i podzieliła go na dwa identyczne trójkąty, każdy o polu równym $\frac{15}{2}$ .

$P_{\bigtriangleup DCN}=P_{\bigtriangleup DLC}=\frac{15}{2}$

Znajdziemy teraz skale podobieństwa trójkątów zakreskowanych do trójkąta $ABC$ .

Skala podobieństwa trójkąta $DRL$ do trójkąta $ABC$ jest równa

$\frac{\frac{2}{5}}{2}=\frac{1}{5}$

a trójkąta $PDN$ do trójkąta $ABC$ jest równa

$\frac{\frac{3}{5}}{2}=\frac{3}{10}$

$\left | PN \right |=\frac{3}{10}\cdot 2z=\frac{3}{5}z$

Możemy teraz zauważyć, że trójkąt $CND$ oraz trójkąt $PDN$ mają taka samą wysokość. Możemy zatem zapisać

$P_{\bigtriangleup DCN}=\frac{1}{2}\cdot \left | NC \right |\cdot h=\frac{15}{2}$

$P_{\bigtriangleup PDN}=\frac{1}{2}\cdot \left | PN \right |\cdot h$

$\frac{P_{\bigtriangleup DCN}}{P_{\bigtriangleup PDN}}=\frac{\frac{1}{2}\cdot \left | NC \right |\cdot h}{\frac{1}{2}\cdot \left | PN \right |\cdot h}$

$\frac{P_{\bigtriangleup DCN}}{P_{\bigtriangleup PDN}}=\frac{ \left | NC \right |}{\left | PN \right |}=\frac{\frac{2}{5}z}{\frac{3}{5}z}=\frac{2}{5}\cdot \frac{5}{3}=\frac{2}{3}$