zadanie 26 (0-3) zbiór rozszerzenie

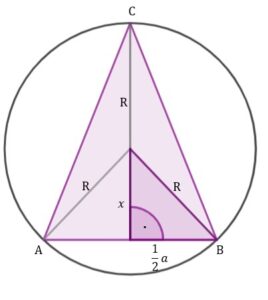
Zróbmy rysunek pomocniczy wiedząc, że $\left | AC \right |=\left | BC \right |$ oraz odległość od środka okręgu do podstawy trójkąta $AB$ jest równa $x$ .

Niech odcinek $\left |AB \right |=a$ .

$P_{\bigtriangleup ABC }=\frac{1}{2}a h$

$h=R+x$

Długość $a$ możemy obliczyć korzystając z twierdzenia Pitagorasa:

$x^2+\left ( \frac{1}{2} a \right )^2=R^2$

$\frac{1}{4}a^2=R^2-x^2\; \; /\cdot 4$

$a^2=4\left ( R^2-x^2 \right )$

Wiemy że długość boku nie może być liczbą ujemną zatem

$a=2\sqrt{R^2-x^2}$

Podstawiając powyższe do wzoru na pole mamy:

$P(x)=\frac{1}{2}\cdot 2\sqrt{R^2-x^2}\cdot \left ( R+x \right )$

$P(x)=\left ( R+x \right )\cdot \sqrt{R^2-x^2}$

Co należało pokazać.

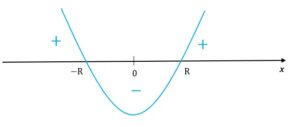
Określmy dziedzinę naszej funkcji $P(x)$

Promień $R$ oraz odległość środka okręgu $x$ od do podstawy trójkąta $AB$ nie mogą być liczbami ujemnymi.

Zatem: $x> 0\; \; \wedge\; \;R> 0\; \; \wedge \; \; R^2-x^2> 0$

$R^2-x^2> 0\; \; \Rightarrow \; \; \left ( R-x \right )\left ( R+x \right )> 0$

Uwzględniając powyższe możemy zapisać:

$R^2-x^2> 0\; \; \Rightarrow \; \; x\in \left ( 0,R\right )$

$P(x)=\left ( R+x \right )\cdot \sqrt{R^2-x^2}$

$D: x\in \left ( 0,R \right )$

Was this helpful?

0 / 0

Dodaj komentarz 0