zadanie 27 (0-6) zbiór rozszerzenie

Ustalmy boki naszego trójkąta bazując na danych z zadania i opiszmy na nim okrąg.

$\left | BC \right |=x$

$\left |AB \right |=2x$

$Obw_{\bigtriangleup ABC}=\left | AB \right |+\left | BC \right |+\left | AC \right |$

$3R=2x+x+\left | AC \right |$

$\left | AC \right |=3R-3x$

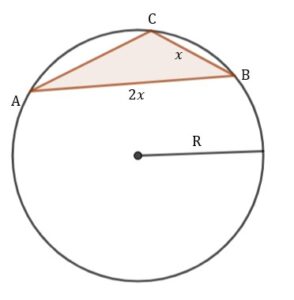Z nierówności trójkąta mamy:

$2x+x>3R-3x$

$6x>3R\; \; /:6$

$x> \frac{1}{2}R$

$2x+3R-3x>x$

$-2x>-3R\; \; /:\left ( -2 \right )$

$x< \frac{3}{2}R$

$3R-3x+x> 2x$

$-4x> -3R\; \; /:\left ( -4 \right )$

$x< \frac{3}{4}R$

Zatem $x\in \left ( \frac{1}{2}R,\frac{3}{4}R \right )$

Skorzystamy z wzoru na pole trójkąta uwzględniający promień okręgu opisanego na trójkącie:

$P_{\bigtriangleup ABC}=\frac{\left | AB \right |\cdot \left | BC \right |\cdot \left | AC \right |}{4R}$

$P_{\bigtriangleup ABC}=\frac{2x\cdot x\cdot \left ( 3R-3x \right )}{4R}=\frac{6x^2R-6x^3}{4}=-\frac{3}{2}x^3+\frac{3}{2}x^2R$

$P(x)=-\frac{3}{2}x^3+\frac{3}{2}x^2R$ dla $x\in \left ( \frac{1}{2}R,\frac{3}{4}R \right )$

Obliczymy następnie pochodną $P'(x)$ oraz jej miejsca zerowe.

$P'(x)=-\frac{3}{2}\cdot 3x^2+\frac{3}{2}\cdot 2xR$

$P'(x)=-\frac{9}{2}x^2+3xR$

$P'(x)=0\; \; \Leftrightarrow \; \; -\frac{9}{2}x^2+3xR=0$

$x\left ( -\frac{9}{2}x+3R \right )=0$

$x=0\; \; \vee \; \; -\frac{9}{2}x+3R=0$

$x=0\; \; \vee \; \; -\frac{9}{2}x=-3R\; \; /\cdot \left (-\frac{2}{9} \right )$

$x=0\; \; \vee \; \; x=\frac{2}{3}R$

Uwzględniając $x\in \left ( \frac{1}{2}R,\frac{3}{4}R \right )$ mamy $x_{0}=\frac{2}{3}R$

$P\left (\frac{2}{3} R \right )= -\frac{3}{2}\cdot \left ( \frac{2}{3}R \right )^3+\frac{3}{2}\left ( \frac{2}{3}R \right )^2\cdot R=-\frac{3}{2}\cdot \frac{8}{27}R^3+\frac{3}{2}\cdot \frac{4}{9}R^2\cdot R$

$P\left (\frac{2}{3} R \right )= -\frac{4}{9}R^3+\frac{2}{3}R^3=\frac{2}{9}R^2$

Zbadajmy przebieg zmienności funkcji

$x\in \left ( \frac{1}{2}R,\frac{3}{4}R \right )$

$P'(x)> 0\; \; \Leftrightarrow \; \; x\in \left ( \frac{1}{2}R ,\frac{2}{3}R\right )$

$P'(x)< 0\; \; \Leftrightarrow \; \; x\in \left ( \frac{2}{3}R ,\frac{3}{4}R \right )$

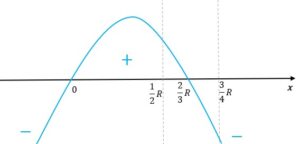Podsumowując $P(x)$ jest rosnąca w przedziale $x\in \left ( \frac{1}{2}R ,\frac{2}{3}R \right ]$ a malejąca w przedziale $x\in\left [ \frac{2}{3}R ,\frac{3}{4}R \right )$ . Oznacza to, że $x=\frac{2}{3}R$ funkcja osiąga maksimum.