zadanie 28 (0-3) zbiór rozszerzeni

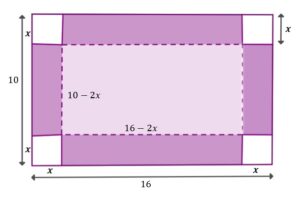
Zacznijmy od uzupełnienia rysunku.

Wiemy, że długość boku nie może być liczbą ujemną, mamy zatem:

$x>0$

$10-2x>0$

$-2x>-10\; \; /:\left ( -2 \right )$

$x<5$

$16-2x>0$

$-2x>-16\; \; /:\left ( -2 \right )$

$x<8$

$x\in \left ( 0,5 \right )$

Obliczmy teraz objętość prostopadłościanu

$V\left ( x \right )=\left ( 16-2x \right )\cdot \left ( 10-2x \right )\cdot x$

$V(x)=\left (160 -20x-32x+4x^2\right )\cdot x$

$V(x)=160x-52x^2+4x^3$

Funkcja opisująca objętość prostopadłościanu jest postaci:

$V(x)=4x^3-52x^2+160x$ dla $x\in \left ( 0,5 \right )$

Obliczymy kolejno pochodną funkcji $V'(x)$ oraz jej miejsca zerowe.

$V'(x)=4\cdot 3x^2-52\cdot 2x+160$

$V'(x)=12x^2-104x+160$

$V'(x)=0\; \; \Leftrightarrow \; \; 12x^2-104x+160=0\; \; /:4$

$3x^2-26x+40=0$

$\Delta =\left ( -26 \right )^2-4\cdot 3\cdot 40=676-480=196$

$\sqrt{\Delta }=14$

$x_{1}=\frac{26-14}{2\cdot 3}=\frac{12}{6}=2$

$x_{1}=\frac{26+14}{2\cdot 3}=\frac{40}{6}=\frac{20}{3}=6\frac{2}{3}$

Uwzględniając dziedzinę $x\in \left ( 0,5 \right )$ mamy $x_{0}=2$

$V(2)=4\cdot 2^3-52\cdot 2^2+160\cdot 2=4\cdot 8-52\cdot 4+320=32-208+320=144$

$V(2)=144$

Zbadajmy przebieg zmienności funkcji

$x\in \left ( 0,5 \right )$

$V'(x)>0\; \; \Leftrightarrow \; \; x\in \left ( 0,2 \right )$

$V'(x)<0\; \; \Leftrightarrow \; \; x\in \left ( 2,5 \right )$

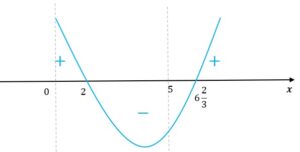Podsumowując $V(x)$ jest rosnąca w przedziale $x\in \left ( 0, 2 \right ]$ a malejąca w przedziale $x\in \left [ 2,5 \right )$ .

Największa objętość pudełka równą $V(2)=144$ otrzymamy dla $x=2$ ponieważ w $x=2$ funkcja ma maksimum.

Was this helpful?

1 / 0

Dodaj komentarz 0