zadanie 29 (0-6) zbiór rozszerzenie

Korzystając z twierdzenia Pitagorasa mamy:

$5^2+d^2=13^2$

$25+d^2=169$

$d^2=144$

$d=12$

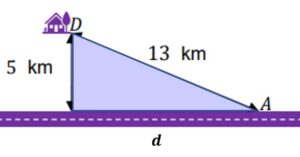Załóżmy, że Janusz cześć drogi pójdzie główną drogą po czym skręci i pójdzie „na skróty” do domu. Zobrazujmy taką ewentualność

$5^2+\left ( 12-x \right )^2=y^2$

$25+\left ( 12-x \right )^2=y^2$

$y=\sqrt{25+\left ( 12-x \right )^2}$

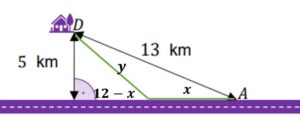Obliczmy teraz czas jaki Janusz potrzebuje na pokonanie kolejnych odcinkach drogi:

odcinek $x$ pokona z prędkością $5\; \mathrm{km/h}$ . Zatem potrzebuje czasu: $t_{1}=\frac{x}{5}$
odcinek $\left (12-x \right )$ pokona z prędkością $3\; \mathrm{km/h}$ . Zatem potrzebuje czasu: $t_{2}=\frac{\sqrt{25+\left ( 12-x \right )^2}}{3}$

Opiszmy funkcją czas potrzebny Januszowi na dotarcie do domu

$t(x)=\frac{x}{5}+\frac{\sqrt{25+\left ( 12-x \right )^2}}{3}$

$t(x)=\frac{x}{5}+\frac{\sqrt{25+144-24x+x^2}}{3}$

$t(x)=\frac{x}{5}+\frac{\sqrt{169-24x+x^2}}{3}$

Określmy dziedzinę naszej funkcji

$12-x\geq 0\; \; \wedge \; \; x\geq 0\; \; \wedge \; \; 25+\left ( 12-x \right )^2\geq 0$

$x\leq 12\; \; \wedge \; \; x\geq 0\; \; \wedge \; \; x\in \mathbb{R}$

$D_{t}:x\in \left [ 0,12 \right ]$

Obliczymy kolejno pochodna naszej funkcji $t'(x)$

$t'(x)=\frac{1}{5}+\frac{1}{3}\frac{1}{2\sqrt{169-24x+x^2}}\cdot \left ( 2x-24 \right )$

$t'(x)=\frac{1}{5}+\frac{2\left ( x-12 \right )}{6\sqrt{169-24x+x^2}}$

$t'(x)=\frac{1}{5}+\frac{\left ( x-12 \right )}{3\sqrt{169-24x+x^2}}$

$t'(x)=\frac{3\sqrt{169-24x+x^2}+5\left ( x-12 \right )}{3\sqrt{169-24x+x^2}}$

$D_{t'}:x\in \left [ 0,12 \right ]$

Obliczymy miejsca zerowej pochodnej:

$\frac{3\sqrt{169-24x+x^2}+5\left ( x-12 \right )}{3\sqrt{169-24x+x^2}} =0$

$3\sqrt{169-24x+x^2}+5x-60=0$

$3\sqrt{169-24x+x^2}=60-5x$

Podnieśmy obustronnie równanie do kwadratu

$9\left ( 169-24x+x^2 \right )=\left (60-5x \right )^2$

$1521-216x+9x^2=3600-600x+25x^2$

$16x^2-384x+2079=0$

$\Delta =\left ( -384 \right )^2-4\cdot 16\cdot 2079=147456-133056=14400$

$\sqrt{\Delta }=120$

$x_{1}=\frac{384-120}{2\cdot 16}=\frac{264}{32}=8\frac{1}{4}$

$x_{1}=\frac{384+120}{2\cdot 16}=\frac{504}{32}=15\frac{3}{4}$

Uwzględniając dziedzinę pochodnej funkcji $D_{t'}:x\in \left [ 0,12 \right ]$

$t'(x)>0\; \; \Leftrightarrow \; \; x\in \left [ 0,8\frac{1}{4} \right )$

$t'(x)<0\; \; x\in \left (8\frac{1}{4},12\right ]$

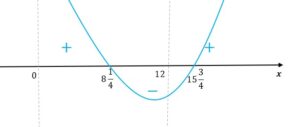Funkcja $t(x)$ jest malejąca w przedziale $x\in \left [ 0,8\frac{1}{4} \right ]$ oraz rosnąca w przedziale $x\in \left [ 8\frac{1}{4},12 \right ]$ . Zatem najmniejszą wartość funkcja osiągnie dla argumentu $x=8\frac{1}{4}$ (maksimum)

$t\left (8\frac{1}{4} \right ) =t\left (\frac{33}{4} \right )$

$t\left ( \frac{33}{4} \right )=\frac{\frac{33}{4}}{5}+\frac{\sqrt{25+\left ( 12-\frac{33}{4} \right )^2}}{3}=\frac{33}{20}+\frac{\sqrt{25+\left ( \frac{15}{4} \right )^2}}{3}$

$t\left ( \frac{33}{4} \right )=\frac{33}{20}+\frac{\sqrt{25+\frac{225}{16}}}{3}=\frac{33}{20}+\frac{\sqrt\frac{{625}}{16}}{3}=\frac{33}{20}+\frac{25}{12}=\frac{99+125}{60}=\frac{224}{60}$

$\frac{224}{60}=3\: h\: 44\: min$

Najkrótszy czas potrzebny Januszowi na dotarcie do domu to $3$ godziny i $44$ minuty.

Was this helpful?

0 / 0