zadanie 30 (0-4) zbiór rozszerzenie

Wiemy że ciężarówka przejedzie $S$ km z prędkością $v\: \mathrm{km/h}$ . Korzystając z wzoru na prędkość

$v=\frac{S}{t}$

czas potrzebny ciężarówce na przejechanie danego odcinka jest równy

$t=\frac{S}{v}$

Wiemy również, że litr paliwa kosztuje $8$ zł oraz, że za godzinę pracy należy zapłacić pracownikowi $42$ złote

Zużycie paliwa opisuje funkcja: $f(v)=7+\frac{v^2}{400}$

Biorąc pod uwagę wskazówkę do zadania i zapiszemy funkcje kosztu $K(v)$ , która będzie uwzględniać wszystkie powyższe warunki

$K(v)=t\cdot \left (f(v)\cdot 8+42 \right )=\frac{S}{v}\left [\left (7+\frac{v^2}{400} \right )\cdot 8 +42 \right ]$

$K(v)=\frac{S}{v}\left [ 56+\frac{v^2}{50}+42 \right ]=\frac{S}{v}\left ( 98+\frac{v^2}{50} \right )$

$K(v)=\frac{98S}{v}+\frac{Sv}{50}$

Z treści zadania wiemy, że minimalna prędkość ciężarówki to $40\: \mathrm{km/h}$ a maksymalna to $80\: \mathrm{km/h}$ .

Zatem $D_{K}:v\in \left [ 40,80 \right ]$

Obliczmy teraz pochodną funkcji $K'(v)$ oraz jej miejsca zerowe

$K'(v)=-\frac{98S}{v^2}+\frac{S}{50}$

$K'(v)=0\; \; \Leftrightarrow \; \; -\frac{98S}{v^2}+\frac{S}{50}=0$

$-\frac{98S}{v^2}=-\frac{S}{50}\; \; /\cdot 50v^2$

$-4900S=-Sv^2\; \; /:\left ( -S \right )$

$v^2=4900$

$v=70\; \; \vee \; \; v=-70$

$K'(v)>0\; \; \Leftrightarrow \; \; v\in \left ( 70,80 \right ]$

$K'(v)<0\; \; \Leftrightarrow \; \; v\in\left [ 40,70 \right )$

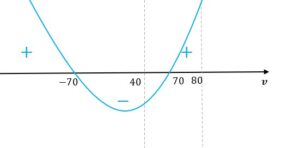Zatem funkcja $K(v)$ jest rosnąca dla $v\in \left [ 70,80 \right ]$ a malejąca dla $v\in \left [ 40,70 \right ]$ . Czyli funkcja $K\left ( v \right )$ przyjmuje wartość najmniejszą (minimum) dla $v=70$ .

Oznacza to, że przy prędkości $v=70$ koszt przejazdu będzie najmniejszy.

Was this helpful?

0 / 0