zadanie 31 (0-6) zbiór rozszerzenie

Obliczymy promień podstawy oraz wysokość stożka. W tym celu uzupełnimy nasz obrazek i skorzystamy z twierdzenia Pitagorasa

$x^2+r^2=1^2$

$x^2=1-r^2$

$x=\sqrt{1-r^2}$

wysokość stożka:

$x+1=\sqrt{1-x^2}+1$

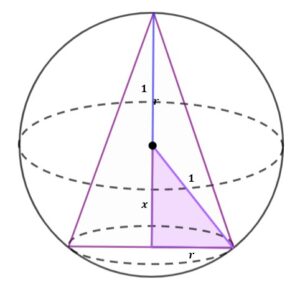Wiemy, że długość promienia podstawy stożka nie może być liczbą ujemną, mamy zatem:

$r> 0\; \; \wedge \; \; 1-r^2> 0$

$r> 0\; \; \wedge \; \; \left (1-r \right )\left ( 1+r \right )> 0$

$r\in \left ( 0,1 \right )$

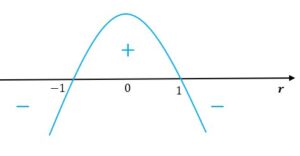Wyznaczmy teraz funkcje opisującą objętość stożka i jej dziedzinę

$V(r)=\frac{1}{3}\pi r^2\cdot \left ( 1+\sqrt{1-r^2} \right )$

$D_{V}:r\in \left ( 0,1 \right )$

Obliczymy następnie pochodną i jej miejsca zerowe

$V'(r)=\frac{1}{3}\cdot 2\pi r\cdot \left ( 1+\sqrt{1-r^2} \right )+\frac{1}{3}\pi r^2\cdot \frac{1}{2\sqrt{1-r^2}}\cdot \left ( -2r \right )$

$V'(r)=\frac{2\pi r}{3}+\frac{2\pi r\sqrt{1-r^2}}{3}\ -\frac{\pi r^3}{3\sqrt{1-r^2}}$

$V'(r)=\frac{2\pi r\sqrt{1-r^2}}{3\sqrt{1-r^2}}+\frac{2\pi r\sqrt{1-r^2}\sqrt{1-r^2}}{3\sqrt{1-r^2}}\ -\frac{\pi r^3}{3\sqrt{1-r^2}}$

$V'(r )=\frac{2\pi r\sqrt{1-r^2}+2\pi r\left | 1-r^2\right |-\pi r^3}{3\sqrt{1-r^2}}$

$V'(r )=\frac{2\pi r\sqrt{1-r^2}+2\pi r \left (1-r^2 \right )-\pi r^3}{3\sqrt{1-r^2}}$

$V'(r )=\frac{2\pi r\sqrt{1-r^2}+2\pi r -2\pi r^3-\pi r^3}{3\sqrt{1-r^2}}$

$V'(r )=\frac{\pi r\left (2\sqrt{1-r^2}+2 -3 r^2 \right )}{3\sqrt{1-r^2}}$

Obliczymy teraz miejsca zerowe pochodnej

$V'(r)=0$

$\frac{\pi r\left (2\sqrt{1-r^2}+2 -3r^2 \right )}{3\sqrt{1-r^2}}=0\; \; /\cdot 3\left ( \sqrt{1-r^2} \right )$

$\pi r\left ( 2\sqrt{1-r^2} +2-3r^2\right )\left ( 1-r^2 \right )=0$

$2\sqrt{1-r^2} +2-3r^2=0\; \; \vee \; \; r=0\; \; \vee \; \; \left ( 1-r \right )\left ( 1+r \right )=0$

$2\sqrt{1-r^2}=3r^2-2\; \; /^2\; \; \; \; \vee \; \; r=0\; \; \vee \; \; r=1\; \; \vee \; \; r=-1$

$4\left ( 1-r^2 \right )=9r^4-12r^2+4\; \; \; \; \vee \; \; r=0\; \; \vee \; \; r=1\; \; \vee \; \; r=-1$

$4-4r^2=9r^4-12r^2+4\; \; \; \; \vee \; \; r=0\; \; \vee \; \; r=1\; \; \vee \; \; r=-1$

$9r^4-8r^2=0\; \; \; \; \vee \; \; r=0\; \; \vee \; \; r=1\; \; \vee \; \; r=-1$

$r^2\left ( 9r^2-8 \right )=0\; \; \; \; \vee \; \; r=0\; \; \vee \; \; r=1\; \; \vee \; \; r=-1$

$r^2=0\; \; \vee \; \; 9r^2=8\; \; \; \; \vee \; \; r=0\; \; \vee \; \; r=1\; \; \vee \; \; r=-1$

$r=0\; \; \vee \; \; r^2=\frac{8}{9}\; \; \; \; \vee \; \; r=0\; \; \vee \; \; r=1\; \; \vee \; \; r=-1$

$r=0\; \; \vee \; \; r=\frac{2\sqrt{2}}{3}\; \;\vee \; \; r= -\frac{2\sqrt{2}}{3}\; \; \vee \; \; r=0\; \; \vee \; \; r=1\; \; \vee \; \; r=-1$

$V'(r)>0\; \; \Leftrightarrow \; \; r\in \left ( 0,\frac{2\sqrt{2}}{3} \right )$

$V'(r)<0\; \; \Leftrightarrow \; \; r\in \left ( \frac{2\sqrt{2}}{3},1 \right )$

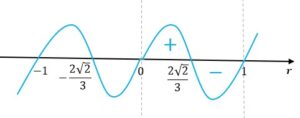Zatem funkcja $V(r)$ rośnie w przedziale $r\in \left ( 0,\frac{2\sqrt{2}}{3} \right ]$ oraz maleje w przedziale $r\in \left [ \frac{2\sqrt{2}}{3},1 \right )$

Oznacza to, że w punkcie $r=\frac{2\sqrt{2}}{3}$ funkcja osiąga maksimum.

Obliczmy $V\left ( \frac{2\sqrt{2}}{3} \right )$

$V\left ( \frac{2\sqrt{2}}{3} \right )=\frac{1}{3}\pi \cdot \left ( \frac{2\sqrt{2}}{3} \right )^2\cdot \left ( 1+\sqrt{1-\left ( \frac{2\sqrt{2}}{3} \right )^2} \right ) =\frac{1}{3}\pi \cdot \frac{8}{9}\cdot \left ( 1+\sqrt{1-\frac{8}{9}} \right )$

$V\left ( \frac{2\sqrt{2}}{3} \right )=\frac{8}{27}\pi \cdot \left ( 1+\sqrt{\frac{1}{9}} \right )=\frac{8}{27}\pi \cdot\left ( 1+\frac{1}{3} \right )=\frac{8}{27}\pi \cdot\frac{4}{3}=\frac{32}{81}\pi$

Czyli największa objętość stożka jest równa $\frac{32}{81}\pi$ i otrzymujemy ją dla promienia długości $\frac{2\sqrt{2}}{3}$

Was this helpful?

0 / 0